I'll take a shot at it with a few assumptions. Since you're talking about contact between macroscopic objects, and the area of the sheets represents the area of contact, we can assume $R>>D>>d$. As has been mentioned in the comments, we cannot extrapolate to infinite sheets or there won't be an electric field.
The method here will be to keep the first sheet fixed, and estimate the potential energy of the second sheet as a function of $D$. The derivative $\frac{dU}{dD}$ will give us the force suffered by it.
Placing the fixed sheet on the x-y plane, with its center on the origin, we have to start by calculating its electric field. We'll restrict ourselves to calculating the electric field it generates on a point that lies on the $z$ axis, a distance $D$ from its center (justified later). For that, we'll assume the sheet is disk-shaped, and treat this dipole disk as a pair of charged disks separated by a distance $d$ that coincide with the planes $z=\pm d/2$. The electric field generated by a charged disk is easy to find on textbooks (and easy to integrate as well), being
$$ E(z) = \frac{\sigma}{2\epsilon_0}\left(1 - \frac{z}{\sqrt{R^2+z^2}}\right).$$
Rewriting it to suit our dipole:
$$ E_T(z) = E(z+d') - E(z-d') = \frac{\sigma}{2\epsilon_0}\left(- \frac{z+d'}{\sqrt{R^2+(z+d')^2}} + \frac{z-d'}{\sqrt{R^2+(z-d')^2}}\right),$$
where $d'=d/2$ and $\sigma = eN$. We could use a couple approximations on the above equation, but they're unnecessary right now. The point is that we know what is the electric field that the fixed sheet generates on the center of the second sheet.
We'll now have to use the approximations. This result is the electric field that's felt by a single dipole on the second sheet. If the sheets were infinite, symmetry would imply that all dipoles on the second sheet are under the same (constant) electric field, and the potential energy per unit area of the second sheet would be $U=\vec{E}_T\cdot\vec{p}\,N = E_T(D)p\,N$. Since $R>>D$, the border effects won't be too relevant, and we'll assume that $E_T$ is constant along the entire second sheet (much like one does inside capacitors). That leads to the total potential energy of the second sheet
$$U(D)=\frac{(pN)^2}{2\epsilon_0d}\left(- \frac{D+d'}{\sqrt{R^2+(D+d')^2}} + \frac{D-d'}{\sqrt{R^2+(D-d')^2}}\right)\pi R^2,$$
as well as the potential energy per unit area
$$u(D)=\frac{(pN)^2}{2\epsilon_0d}\left(- \frac{D+d'}{\sqrt{R^2+(D+d')^2}} + \frac{D-d'}{\sqrt{R^2+(D-d')^2}}\right).$$
Taking the first derivative with respect to $D$, will give us the force and the pressure (respectively) that the fixed sheet applies on the second sheet.
Update
Here go the answers:
$$F=\frac{\pi(RpN)^2}{2\epsilon_0d}(G_- - G_+)$$
$$P=\frac{(pN)^2}{2\epsilon_0d}(G_- - G_+)$$
$$G_\pm = (R^2 + (D\pm d/2)^2)^{-.5} - (D\pm d/2)^2(R^2 + (D\pm d/2)^2)^{-1.5}.$$
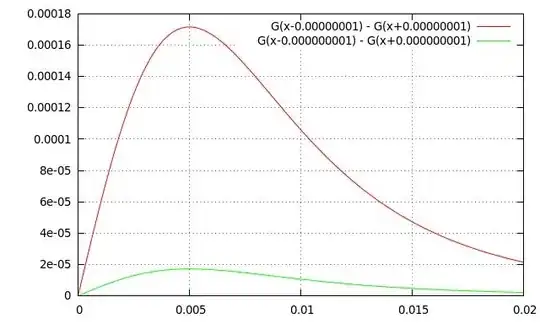
From what I can tell, these are the Force and Pressure that the question asks for. Below are a couple of plots for $G_--G_+$ (measured in $1/m$), just multiply their $y$ values by $\frac{(pN)^2}{2\epsilon_0d}$ to get the pressure. The $x$ axis is $D$ measured in $m$.
This plot uses $R=1mm$. Green line is $d=1nm$, Red line is $d=10nm$.
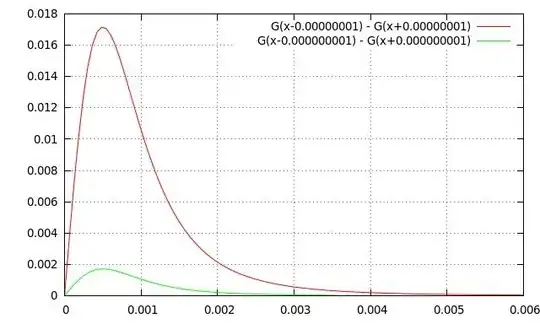
This plot uses $R=1cm$. Green line is $d=1nm$, Red line is $d=10nm$.