1

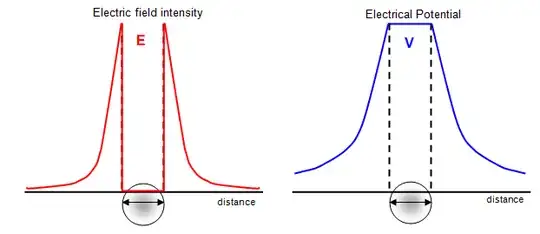
As a general concept, potential energy of a configuration is equal to the work done by an external force against an existing conservative force. It is this work done that gets stored in the body as its potential energy. This way I can calculate the electric potential at any particular point in an electric field.

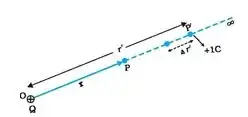
Let's calculate the potential of the following configuration: enter image description here

The charge $q$ (i.e. 1C) is being moved towards $Q$, against the electrostatic force of repulsion due to $Q$. Let it be moved by a small distance $dr$ towards $Q$, so that the work done by external force is $F.dr$, which must come positive as the external force and the displacement are along the same direction. However, this conclusion would give me a negative electric potential on integration for limits $infinity$ to $r$. The book says electric potential must come positive, where have I gone wrong? Some books try to explain this by calculating the work done by electric force and not the one due to external force.

It may be a possible duplicate of Why is electric potential positive? but I haven't got answers at that place as well

Community
  • 1
Swami
  • 1,917

2 Answers2

3

I believe you are confusing the work done by the electric field with the work done on the particle.

  • By the electric field: The radial force of the electric field is always pointing outwards, and the displacement of the charge in this case is going inward. Thus, the integral you've specified will be negative. That is, the work done by the electric field is negative.

  • On the Particle: The force that must be applied to the charge (ignoring gravity, relativity, induced vector-potential, etc.) to get it from infinity to the radial distance $r$ is, at the very least, equal and opposite to the force of the electric field acting on the charge. Thus, it is always pointing inwards. Given that the charge is going inwards, the work integral will come out positive.

enter image description here

Arturo don Juan
  • 5,489
  • 7
  • 37
  • 81
2

The electric potential can be negative.

Both in difference and absolutely if you have chosen a gauge. To see that this must be so, just replace the charge distribution (not the test charge, all the others...) with one that has the opposite sign.

dmckee --- ex-moderator kitten
  • 87,238