At what point (or distance) from the axis of rotation, does force applied on a rigid body stop translating and purely rotating the body? Can such a point even exist? Does the body always have to translate?
This question assumes that the body is in empty space and unattached.
The only way to purely rotate a rigid body about its center of mass is to apply a pure torque (no net force). If the net force applied is zero then the center of mass is not accelerating.
However and combination of translation and rotation of the center of mass can be viewed as a pure rotation about the instant center of rotation. So to effectively answer your question, a force not through the center of mass will rotate the body about a specified point.
For planar case see: https://physics.stackexchange.com/a/86996/392
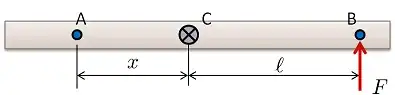
The point of rotation A is defined by the distance $x$ as
$$x = \frac{I_{cm}}{m \ell}$$
If you want to go a little deeper then see: https://physics.stackexchange.com/a/81078/392
Note that these two statements are equivalent:
- A pure force thorugh the center of gravity (with no net torque) will purely translate a rigid body (any point on the body).
- A pure torque any point on the body (with no net force) will purely rotate a rigid body about its center of gravity
If there is no fulcrum, if there is no fixed pivot, a body will always translate.
Such point does not exist. If the body is free, it can only translate but can never only rotate: if the impulse is at the Center of Mass linear velocity will be 100% , the minimum percentage of translational velocity is 25%, and it is reached at one tip of the rod. No matter what is the length or the mass of the rod, there is no point where linear velocity can be zero and rotational velocity 100%
