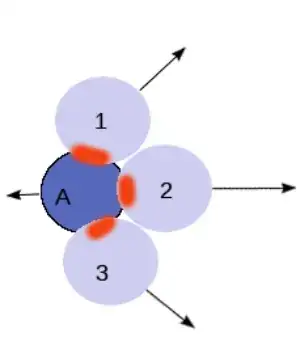
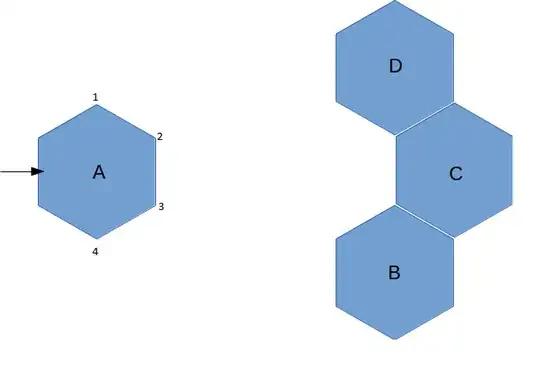
Here is how you deal this this problem as a system of equations. For each contact pair assign a normal direction $\hat{n}_k$ and and impulse $J_k$. The possible contacts are AB, AC, and AD. We can introduce symmetries and simplifications later.
The initial velocity if body A is $v_A$ along the horizontal axis, and after the collision it is $v_A + \Delta v_A$. From the change in momentum you can work out
$$ m \Delta v_A = -J_{AB} \frac{1}{2} -J_{AC} - J_{AD} \frac{1}{2} $$
where the factors of 1/2 come from $\cos 60°$. This is simplification of the general equation $$m_i \Delta \vec{v}_i = \sum_k \hat{n}_k J_k$$ when projected along the x-axis.
Now we look at the momentum change of body C along the horizontal axis also
$$ m \Delta v_C = J_{AC} $$ and the momentum change for the rest of the bodies is measured along the contact normals (60° from horizontal) as $$m \Delta v_B = J_{AB} \\ m \Delta v_D = J_{AD}$$.
For fun I am including the possibility of inelastic collision with $\epsilon$ the coefficient of restitution. The collision rules are expressed along the contact normals where the final relative speed is a negative fraction of the impact relative speed
$$\begin{align}
\frac{1}{2}(v_A+\Delta v_A)-(v_B+\Delta v_B) & = -\epsilon (\frac{1}{2}v_A-v_B) \\
(v_A+\Delta v_A)-(v_C+\Delta v_C) & = -\epsilon (v_A-v_C) \\
\frac{1}{2}(v_A+\Delta v_A)-(v_D+\Delta v_D) & = -\epsilon (\frac{1}{2}v_A-v_D)
\end{align}$$
In the above three equations the changes of speed as substituted from the momentum equations such as $$\begin{align}
\Delta v_A &= (-J_{AB} \frac{1}{2} -J_{AC} - J_{AD} \frac{1}{2})/m \\
\Delta v_B &= J_{AB}/m \\
\Delta v_C &= J_{AC}/m \\
\Delta v_D &= J_{AD}/m \end{align} $$
The above becomes a 3×3 system of equations for the impulses
$$ \frac{1}{m} \begin{bmatrix}
-\frac{5}{4} & -\frac{1}{2} & -\frac{1}{4} \\
-\frac{1}{2} & -2 & -\frac{1}{2} \\
-\frac{1}{4} & -\frac{1}{2} & \frac{-5}{4} \end{bmatrix}
\begin{pmatrix} J_{AB} \\ J_{AC} \\ J_{AD} \end{pmatrix} = -(\epsilon+1)
\begin{pmatrix} \frac{1}{2}v_A-v_B \\ v_A-v_C \\ \frac{1}{2} v_A - v_D
\end{pmatrix}$$
When B, C and D are at rest initially the above is solved for
$$ \begin{align} J_{AB} &= (\epsilon+1) \frac{m v_A}{5} \\ J_{AC} & = (\epsilon+1) \frac{2 m v_A}{5} \\ J_{AD} &= (\epsilon+1) \frac{m v_A}{5} \end{align} $$
Now the final velocities are found by
$$\begin{align} v_A+\Delta v_A & = \frac{v_A (2-3\epsilon)}{5}\\
v_B+\Delta v_B &= \frac{v_A (\epsilon+1)}{5} \\
v_C+\Delta v_C &= \frac{2 v_A (\epsilon+1)}{5} \\
v_D+\Delta v_D &= \frac{v_A (\epsilon+1)}{5} \end{align}$$
For an elastic collision ($\epsilon=1$) the final speed of B is $v_B+\Delta v_B = 0.8 v_A$.
NOTE: Solution of n-body collision https://physics.stackexchange.com/a/91069/392