Deriving the Lorentz factor $\gamma$

Question

Recently, I learned how to derive $E_0 = m_0c^2$. However, to do so, one must accept the relativistic mass equation. How does one derive the Lorentz factor $\gamma$?

Answer 1

After some searching, I found a very simple way to do so.

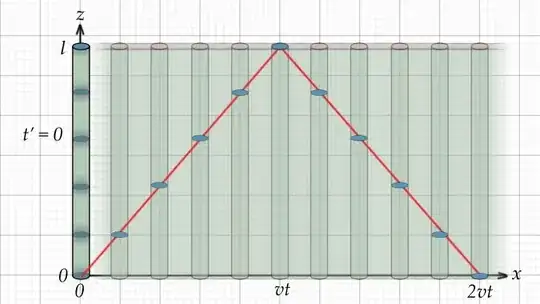
The blue disks shows show light traversing up a rod. If the rod were stationary then the light would reach the top in ct where t starts at t' = 0. However, with the horizontal motion of the rods, the light takes a diagonal path, indicated by the red line. By the Pythagorean Theorem, we get $$d^2 = l^2 + (vt)^2$$ (d being the distance of the first half of the red line)

Since l = ct, we get $$d^2 = c^2t^2 + v^2t^2$$

Since d = ct', we get $$c^2t'^2 = c^2t^2 + v^2t^2$$

Solving for t', we get $$t' = \dfrac{t}{\sqrt{1-\dfrac{v^2}{c^2}}}$$

Divding by t, we get $$\frac{t'}{t} = \dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}$$

Which is the Lorentz Factor

Answer 2

We can use the fact that the speed of light is the same in every inertial reference frame: $$c=\frac{dx}{dt}=\frac{dx'}{dt'}$$ From that we can construct the space-time interval: $$(ds)^2=c^2dt^2-dx^2$$ The space-time interval is invariant in every inertial reference frame. $$(ds)^2=(ds')^{2}$$ In proper frame, the space-time interval has the following form: $$(ds)^2=c^2dt^2$$ where $dt$ is usually written as $d\tau$ and it is called the proper time. We know that the space-time interval is the same in every inertial reference frame, so we can write that the space-time interval in our proper frame is equivalent to any other inertial reference frame: $$c^2d\tau^2=c^2dt^2-dx^2$$ Divide both sides by $c^2dt^2$: $$\frac{d\tau}{dt}=\sqrt{1-\frac{v^2}{c^2}}$$ so: $$d\tau=dt\sqrt{1-\frac{v^2}{c^2}}$$ or: $$dt=\frac{d\tau}{\sqrt{1-\frac{v^2}{c^2}}}=\gamma\cdot d\tau$$

Answer 3

I think the Lorentz factor is wrong because it's based on Einstein's 2nd postulate which implies that the speed of light is constant irrespective of the motion of the emitting body. However, most people apply it as if it were constant for all observers.

In any case, it's a postulate i.e. an assumption. Einstein used the speed of light as constant after Maxwell calculated its value from the permeability and permittivity of free space which are constants and cannot vary under any circumstances.

If you move an electric charge in front of a magnetic field detector, it would detect the presence of a magnetic field. More importantly, if you move a magnetic field detector in front of a static charge, it'll also detect a magnetic field. Hence, electromagnetism is subject to relativity as Galileo implied. Well, he said that everything is relative.

Now light is made of photons which are electromagnetic particles. That means that velocity will interfere with the strength of the magnetic field. And it's either the velocity of light relative to the observer or the observer's velocity to that of light - they're equivalent. Maybe that's how the Doppler shift happens. We don't know what wavelength refers to. Maybe it's inversely proportional to the strength of the magnetic field component of the electromagnetic field.

Keeping the strength of the magnetic component of the electromagnetic field invariant across all frames of reference, may be a mistake. This means that all forms of relativity may be wrong. I'm certain of it. It could turn out that Galilean transformation was the right one to use after all.