Torque on a disc?

Question

In the following diagram:

Point(c) is a going into the page and attached to the disc, Point(c) applies a torque($\tau$) to the disc, and it starts to rotate due to that torque.

And if point(c) was move from the center to the far left like so:

The disc will still rotate, around point(c). What if we added an equal point with the same torque in the opposite position(far right), what is the result?

I think the disc now will be at rest, unable to move. However, I could not explain why...

Answer 1

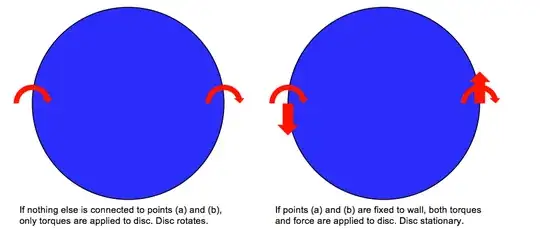
If you attached two flywheels through a motor to the disk at the positions you show, and the motors start spinning in the same direction, then conservation of angular momentum tells us that as the flywheels spin clockwise, the disk must (and will) rotate counterclockwise.

However - if you attach the motors to an external structure, you are preventing rotation. I think that's what you inadvertently did in your original experiment and why you were getting confused (per your comment under ja72's answer).

UPDATE

The laws of motion that apply in this instance can be summarized as follows:

• the center of mass will move as though the vector sum of all forces acts there
• the angular momentum of the object will change with the sum of all torques multiplied by their duration: $$\Delta L = \sum \Gamma \Delta t$$ regardless of the axis about which the torque acts.

This second point is the one you appear to be struggling with. But you can think of it as follows: if you have a floating disk, and you have people standing on that disk with everything stationary, there is no net angular momentum. Now regardless of what the people do, the SYSTEM (people plus disk) must still have net zero angular momentum. So if two people start to spin clockwise about their own axis, the disk must start to spin counterclockwise. Let's see how that works in practice - put them with their feet apart on the disk:

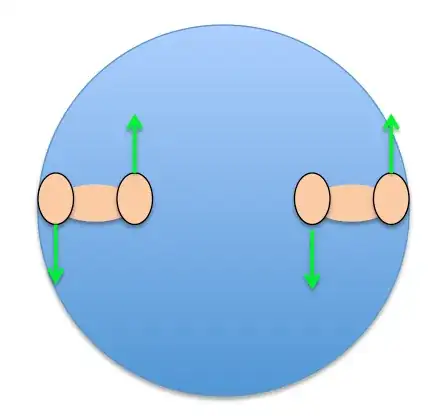
Both are trying to rotate, and so they push forward with their right foot and back with their left. But if you look closely you see that there are now two sets of torque: the left foot of the right hand person and the right foot of the left hand person make a pair that is centered about the center of the disk, and the other feet make another pair in the opposite direction. Now the force is the same but the distance is different, so there will be a net torque on the disk equal to the sum of the two torques applied by the two persons.

Take a bit of time and look at this picture; I think it should clear up your confusion.

Answer 2

On a free floating body, if a pure torque is applied (with net zero force) then the body is going to rotate about it's center of mass (see https://physics.stackexchange.com/a/81078/392). This is regardless of where the torque is applied, or how many torques are applied. If the net force is zero then the center of mass will not move.

Now if C or A or B are joints, besides torques they also supply reaction (support) forces in order to maintain the kinematic relationships. So a joint not at the center of mass will need an in-plane force to make the center of mass rotate about the joint.

In the last case, there is no motion which can make the disk rotate about A and B at the same time. To impose that the linear velocity is zero on A and on B at the same time means the body will not move. The body is overconstrained.

For planar bodies their only possible kinematics are:

1. No motion at all (fixed)
2. All points move with the same non-zero velocity (translation)
3. All points rotate about a single point (rotation about instant center)

The instant center may lie on the body or outside the body. Its location can change with time, but at any instant of time there is only one point a body can rotate about.

See http://en.wikipedia.org/wiki/Instant_centre_of_rotation for more details.

Answer 3

By saying point(c) (or any of the other points) applies a torque on the disc, it sounds like point(c) is a small physical body (If point(c) exerts a torque on the disc, then disc must exert a torque on point(c)) I'm going to assume that the mechanism by which point(c) causes a torque on the disc is a motor connecting point(c) and the disc.

So, if points (a) and (b) are not connected to anything else apart from the disc via motors, then each point will exert a torque on the disc, and the disc will exert equal and opposite torques on the points. Both torques applied to the disc are in the same direction, and so will add together. As there are no other forces or moments being applied anywhere, this means the disc will rotate one way, and the points will rotate the other way (assuming both points apply torques of the same direction on the disc). This seems to make sense if you consider the conservation of angular momentum (not moment of momentum).

If, however, the two points are fixed in space (as if those points are both attached to a rigid wall), then those points will have to be in equilibrium. This means there will be reaction forces to keep the points fixed, and if the points are held fixed, then the points will not only apply torques but also forces on the disc, such that the disc is also held in equilibrium. Net force and torque of that system = 0.

Here is a diagram showing the forces and moments applied to the disc for both cases: