What should we do If we wanted to increase the angular velocity of a planet?

Question

We could hit it with really fast objects, but could we manipulate the orbit of a large satellite to speed up its rotation?

What would be the easiest way?

Answer 1

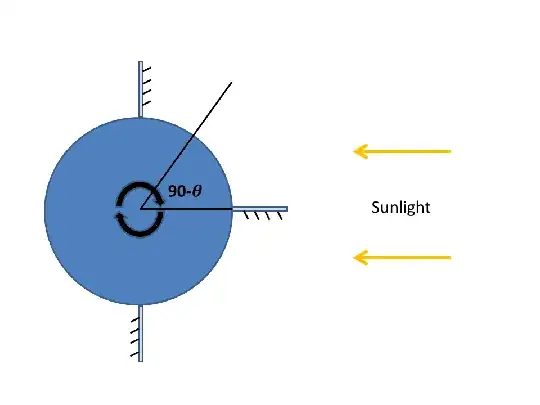
Cover it in mirrors that are highly reflective on one side and painted black on the other. Position the mirrors so that the "faces" are perpendicular to the surface. A sketch is below (I have only shown three mirrors, the idea is that you would cover the planet with them, but they will be most effectively placed close to the equator).

The plan is that each reflective side feels a force due to the radiation pressure from the planet's Sun. If the faces are perfectly reflective the force is of magnitude $2 F A \cos^2 \theta/c$ directed tangentially to the surface, where $F$ is the flux (in Watts per square metre), $A$ is the mirror area and $\theta$ is the angle of incidence, $c$ is the speed , the of light, and the factor of 2 arises fro the perfect reflection. This exerts a torque $T = 2FAr\cos b \cos^2\theta/c$, where $r$ is the planetary radius and $b$ is the latitude of the mirror (I am going to assume for simplicity that the rotation axis of the planet lines up with its orbital axis). We position the mirror so that this torque acts to accelerate the rotation.

Now as the planet rotates, what was the mirrored side of the mirror, then presents its black (totally absorbing face) to its Sun. In that case the torque will be $ T = FA r \cos b \cos \theta/c$. This torque acts against the rotation.

So if we group the mirrors by pairs, with equal $\theta$ but on opposite sides of the "substellar" point, the net torque due to each pair is $$T_{\rm net} = \frac{FA r \cos b}{c} \cos\theta (2\cos\theta -1)$$ and ranges from $FA r \cos b/c$ when the pair of mirrors are at right angles to the incoming radiation ($\theta = 0$), to zero when $\theta=\pi/2$.

If we let there be an equal number of mirrors per unit longitude and also just have them at the equator with $b=0$, the average net torque per pair (assuming the mirrors can only be irradiated for $0<\theta < \pi/2$, and if I've done my Maths right) is $$T_{\rm ave} = (1 - 2/\pi) \frac{FAr}{c}$$ So you multiply this by the number of mirror pairs to get the total torque on the planet.

Would it work? Well to put some numbers in, for mirrors that were prefectly reflective/absorbing placed at the equator of the Earth, each pair would give an average torque of 4.65 Nm per unit area. So a million pairs, each of 1 square metre, provides a torque of $5\times10^{6}$ Nm.

Pathetic! The moment of inertia of the Earth is $\sim 10^{38}$ kg m$^2$, so this torque would take longer than $10^{17}$ years to speed up the Earth's rotation rate by 1%.

The smaller the object, the more effective this method becomes. The torque varies as $r$, whilst the moment of inertia varies as $r^2$. However you also have to factor in how many mirrors you can place around the circumference, which will be limited by $r$. So if you have reached this limit, then there will be no efficiency gain for smaller objects.

Answer 2

Start digging at the equator and move all the dirt to the polar regions. This will decrease the moment of inertia of the planet about its spinning axis. Due to the conservation of angular momentum this will result in an increase in angular velocity, akin to a figure skater who retracts her arms while spinning.