Can someone explain to me when do I use this formula
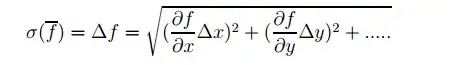
...and when do I use this one?
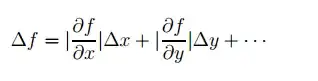
Can someone explain to me when do I use this formula
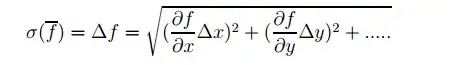
...and when do I use this one?
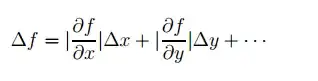
You use the first formula you gave when you have (entirely) uncorrelated errors where the standard variances (the squares of the standard deviances) add. Gaussian distributions of errors are usually assumed.
You might use the second formula if your errors are perfectly correlated, but even then only as a worst-case measure (if you know the correlation, you in some cases a minus sign would be technically appropriate when one error acts to partially cancels the other). In practice, it really only makes sense if you use it as an upper bound estimate where you want to cover for the possibility that you have the worst possible correlation between errors. Note that this will mess up your statistics: If your worst-case error estimate does not overestimate your errors, you either have the worst case or you have made an error!
Using such worst-case estimate may be a good idea if you cannot justify that errors are not correlated. But it is important to realize that now you are making very different statistical statements to usual error estimation. The proper way forward, if you want actual error estimates, would be to determine the correlation, which leads you to error ellipses.