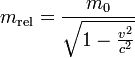I'll give this a shot. I think I follow what you're asking.
I'm thinking of the to-be-fissioned-away material as a mass traveling at the speed of light in some sense,
In a sense that's true, but it's probobly good to keep in mind that time isn't a dimension quite like the other 3 and traveling through time isn't exactly moving, so in a sense it's true mass at rest is traveling at the speed of light through time - as in the link you posted, but it's only true in a certain sense, I think.
So when some of that vast kinetic energy gets redirected into our spatial dimensions
Here, I think we run into a problem. I don't think it's accurate to think of moving through time as kinetic energy. Kinetic energy is probobly limited to the 3 spacial dimensions.
Lets take an example, or thought experiment. First, the energy of motion: 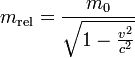
You have 2 identical objects, each exactly 1 KG of rest mass. 1 object is still, the 2nd object is moving at 1/2 the speed of light. (We're ignoring relative motion which might ask - how do you know which object is moving). So, the 2nd object experiences measurable mass increase and time dilation at this speed, an increase of about 15.47% in each. But in this thought experiment, it's no longer moving at the speed of light through time, so by the "speed of light through time" kinetic energy argument, it should lose rest energy as it gains energy of motion, but that's not correct. It has the identical rest mass/rest energy moving or still.
A nuclear bomb, for example, traveling at near the speed of light would have the same explosive energy as a bomb that was still. It would neither gain nor lose explosive energy, but the 2 bombs would have very different velocity through time. A bomb moving at high speed would appear to explode more slowly to an observer, but it would explode with the same energy.
Velocity through time doesn't affect rest energy. I think Lemon is correct, it shouldn't be interpreted that way.
That said, I think a lot of people have noticed the similarity between E=1/2 M V^2 and E=MC^2.
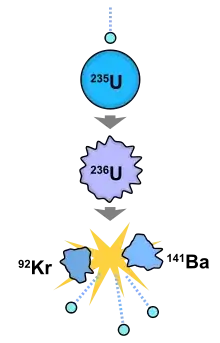
What actually happens in the explosion of a nuclear bomb is the nuclear energy inside the nucleus of the atoms is released. Nuclear bonds are broken and reformed when U235 splits, kind of similar to what happens in combustion when molecular bonds are broken and reformed and hydrocarbons and Oxygen are turned into water and CO2.
In the nuclear explosion, no protons and neutrons are destroyed or changed (though some protons/neutrons change through beta decay, but that's not the explosion and a small fraction of the energy released. The explosion itself is just a release/change of binding energy inside the nucleus. This energy is already traveling at the speed of light, well, kind of, in the form of gluons/the strong force inside the nucleus, but it takes place only over short distances. The nuclear explosion takes energy that's available in the nucleus and turns it into gamma rays, heat and explosive force - things we see and feel, so the actual reaction just turns gluon energy into photon energy (and some kinetic energy). The energy is already there and already moving at the speed of light just trapped in the nucleus of the uranium atom.
Not sure that helps, it's kind of how I look at it, and if that's not right, I welcome correction, but I think that's the gist of it.