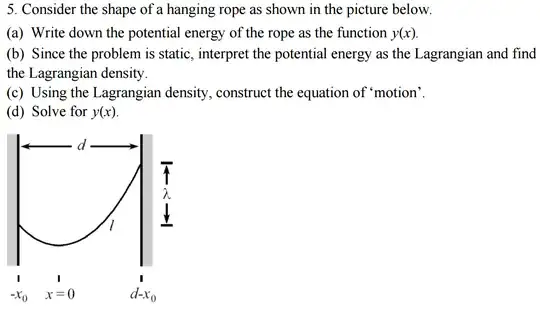
for this one, I can only do the first(a) $$V_{total}=\frac{mg}{l} \int_{x_0}^{d-x_0}{y(x)\sqrt{1+(\frac{dy(x)}{dx})^2}}dx$$
and have no idea about others.

for this one, I can only do the first(a) $$V_{total}=\frac{mg}{l} \int_{x_0}^{d-x_0}{y(x)\sqrt{1+(\frac{dy(x)}{dx})^2}}dx$$
and have no idea about others.
(a) Write down the potential energy of the rope as the function $y(x)$.
You're almost right, up to a minus sign in the limits of the integral: $$V=\dfrac{mg}{l}\int_{-x_0}^{d-x_0}y(x)\sqrt{1+y'^2}\ dx$$
(b) Since the problem is static, interpret the potential energy as the Lagrangian and find the Lagrangian density.
The Lagrangian is usually given by $L=T-V$. Since the problem is static, there is no kinetic energy and $T$ vanishes. Therefore: $$L=-V=-\dfrac{mg}{l}\int_{-x_0}^{d-x_0}y(x)\sqrt{1+y'^2}\ dx$$ Now, the Lagrangian density $\mathcal{L}$ is related to the Lagrangian $L$ by: $$L=\int\mathcal{L}\ dx$$ Such that: $$\mathcal{L}=-\dfrac{mg}{l}y\sqrt{1+y'^2}$$
(c) Using the Lagrangian density, construct the equation of motion.
The Euler-Lagrange equation for $\mathcal{L}(y,y',x)$ is: $$\dfrac{d}{dx}\dfrac{\partial\mathcal{L}}{\partial y'}-\dfrac{\partial\mathcal{L}}{\partial y}=0$$ Plugging in $\mathcal{L}$: $$\dfrac{d}{dx}\left[\dfrac{yy'}{\sqrt{1+y'^2}}\right]-\sqrt{1+y'^2}=0$$ which gives: $$\left[\dfrac{y'^2}{\sqrt{1+y'^2}}+\dfrac{yy''}{\sqrt{1+y'^2}}-\dfrac{y(y')^2y''}{(1+y'^2)^{3/2}}\right]-\sqrt{1+y'^2}=0$$ After some manipulations and simplifications: $$\dfrac{yy''}{(1+y'^2)^{3/2}}-\dfrac{1}{\sqrt{1+y'^2}}=0$$
(d) Solve for $y(x)$.
Multiplying through by $y'$ yields: $$\dfrac{yy'y''}{(1+y'^2)^{3/2}}-\dfrac{y'}{\sqrt{1+y'^2}}=\dfrac{d}{dx}\left[\dfrac{y}{\sqrt{1+y'^2}}\right]=0$$ Integrating with respect to $x$: $$\dfrac{y}{\sqrt{1+y'^2}}=C_1,\quad C_1\in\mathbb{R}$$ which you may recognize as the first-order differential equation for a catenary, such that we get: $$y=C_1\cosh\left(\dfrac{x+C_2}{C_1}\right),\quad C_2\in\mathbb{R}$$ All that is left to do is to find $C_1$ and $C_2$ from the boundary conditions on $y(x)$.