0

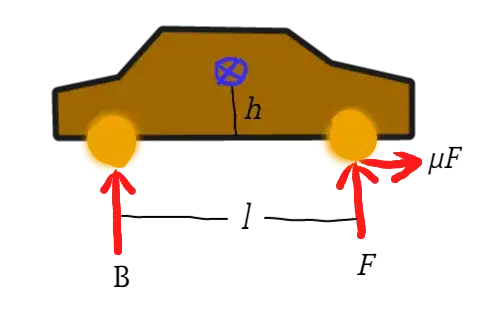
I'm in engineering school and we have a project: we have to build a amphibioues vehicle; I'm looking for a formula.

Our vehicle has to go as far as possible with its unique source of energy, a spring. But if this spring is very powerful then our vehicle might skid.

I searched and found a formula that related the best velocity to go as further as possible :

a_max = μg

With:

  • $R$ the radius of a wheel
  • $\mu$ the coefficient of friction
  • $m$ the mass
  • $I$ the moment of inertia

The problem is we are looking for a velocity (without t) to calculate the ratio to transmit to the gear system.

We found the equation for the acceleration but not the velocity, that what we are looking for.

user1892467
  • 1

3 Answers3

1

I don't think that equation is right. $F_{max} = \mu mg$, so $a_{max} = \mu g$.

Where are you getting velocity from? The spring doesn't move at a constant velocity, does it? You need to use the spring's maximum torque and work out how to weaken it so the final acceleration is sufficiently low.

Why are you trying to make it as fast as possible? If you're going for distance, you have to minimize losses due to friction. Slower would generally be better, although at some point the friction from the gearbox will cause problems.

DanielLC
  • 1,699
0

If the vehicle has 4 wheels, and only 2 have traction then the formula is

$$ \begin{cases} a_{max} = \gamma \mu g & \mbox{RWD}\\ a_{max} = (1-\gamma) \mu g & \mbox{FWD} \end{cases}$$

where $\mu$ is the traction coefficient, $g$ is gravity and $\gamma$ is the %weight on the back wheels. So if the weight distribution is 60%/40% front to back, then $\gamma=0.4$

To get a level up in detail, if the height of the center of mass to the wheel axle is $h$ and the wheelbase is $\ell$ then the maximum acceleration is

$$ \begin{cases} a_{max} =\frac{\ell}{\ell-\mu h} \gamma \mu g & \mbox{RWD}\\ a_{max} = \frac{\ell}{\ell+\mu h} (1-\gamma) \mu g & \mbox{FWD} \end{cases}$$

If you have All Wheel Drive (AWD) then $a_{max} = \mu g$.

I got to this with a crude free body diagram and the equations of motion.

fbd

John Alexiou
  • 40,139
-1

You cant

avoid skidding by an equation.

Would You glue a paper with that formula to Your car?

You avoid skidding by using the appropriate tires for the floor.

Look here for a solution for a car going as far as possible:

en.wikipedia.org/wiki/Mousetrap_car

Georg
  • 6,965