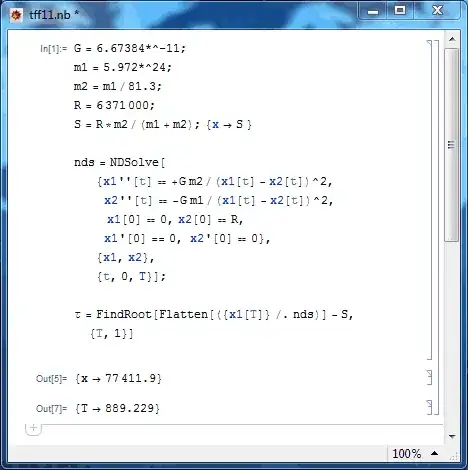
I am trying to program a $n$-body problem simulation. To calculate the position and velocity after a time-step I want to split it in multiple 2 body problems. Now I am stuck, trying to find the velocity and position of two bodies (ignoring all the others) after one time-step with given mass, start position and velocity.
I am able to calculate the force between the two, but I am unable to solve the differential equation $$ \ddot{\vec{r_{12}}(t)} = G M \frac{\vec{r_{12}(t)}}{|\vec{r_{12}(t)}|^3} \\ M := m_1 + m_2 \\ \vec{r_{12}(t)} := \vec{r_1}(t) - \vec{r_2}(t) $$
to calculate the position relative to each other. What is $\vec{r}(t)$ and how can I calculate it? And is there another and maybe faster way to get the positions and velocities?
Edit: As @Sofia pointed out, this was not clear: $\vec{r_1}$ and $\vec{r_2}$ are the location vectors of the two masses.