Effect of gravity upon light and bagels

Question

According to this question and this web site, photons undergo twice the deflection from gravitational fields as do physical objects.

However, the weak equivalence principle states that locally, everything falls at the same rate.

Let's consider the following thought experiment. We place two parallel perfect mirrors in a uniform gravitational field. Between these mirrors we place a bagel so light can travel through the hole. We zap a laser through the hole just as we drop the bagel: the light and bagel are falling together.

In the bagel's reference frame, it seems that we should see the light travel perpendicularly back and forth through the hole, so the light would stay within the hole (ignoring divergence of the beam) until the bagel hits the bottom. It's not completely local, but pretty close.

But a perfect mirror should only fold the trajectory of the photon, so an external observer should see the light deflected at twice the rate of the bagel. Thus, the external observer should see the laser drift lower inside the hole and eventually hit the bagel.

These two predicted observations clearly cannot be reconciled. What actually happens? (For instance, does the bagel-frame no longer think the mirrors are perpendicular, and the non-perpendicularity works out such that the answer does not depend on the distance between mirrors?)

Answer 1

Someone else with knowledge of the mathematical details may be able to say more, but I think the statement that the deflection of light is twice the Newtonian value is just looking the initial angle that the light approaches the gravitating body from far away, at comparing with the final angle once long after it has passed the body and is far away again--in other words, talking about the change in direction over a large region of curved spacetime. This is illustrated for example in Fig. 6.6 on p. 144 of Wald's textbook General Relativity here:

Wald also mentions on that page that the calculation is "for a light ray initially in the asymptotically flat region ($r > > M$)". Wald also says that what they are calculating is "the change, $\Delta \phi = \phi_{+ \infty} - \phi_{- \infty}$, in the angular coordinate $\phi$ of a light ray in the Schwarzschild geometry"--here $\phi_{- \infty}$ should refer to the angle of the light ray in the limit of large times before its closest approach to the gravitating body, and $\phi_{+ \infty}$ should refer to the angle in the limit of large times after its closest approach. When a curved spacetime like the Schwarschild geometry is asymptotically flat, that means it approaches flat spacetime at large distances from some central region--that it's possible to find a coordinate system where, as it says here, the metric will take the form $ds^2 = dt^2 - dx^2 + dy^2 + dz^2$ plus some extra terms that depend on the radius $r$ from the gravitating mass, such that the additional terms "vanish in the limit $r \to \infty$, and the metric will have the form of the Minkowski metric in an inertial frame." So in this limit light should move in a straight line at a constant speed of c, and thus it's straightforward to define the change in angle in the limit of large times before and after its closest approach to the gravitating mass, when it will be in regions that approach being perfectly flat. But this assuming that the light is traveling on a single geodesic the whole time, rather than on a zigzag bouncing between mirrors, where each path between the mirrors is a geodesic but the larger zigzag is not. So that's one way of answering your question--the claim about deflection is about the large-scale deflection of a single geodesic, and thus just wouldn't apply to a zigzag path like the one you imagine.

Still, we could modify your thought experiment by imagining that there were no mirrors, but the light ray was traveling through a series of many donuts, traveling perpendicular to the plane of each donut's circumference as it passed through it, in the local inertial frame where the donut is at rest. Then the equivalence principle would demand that in a different local inertial frame where the donut was moving in some direction that lay in the plane of its circumference, the component of the light ray's velocity in that direction would be identical to the donut's, so for example if a local observer saw the donut moving "downward" at constant velocity they would say the component of the light ray's velocity in the "downward" direction was the same.

But if you want to use the equivalence principle, it can only be applied in the limit as the region of spacetime containing the events you are interested becomes very small. This requires not only that the distance between the mirrors is small, but also that the period in which you observe the light bouncing back and forth is small--as it says at the end of this article, the most precise form of the equivalence principle would be:

Within an infinitely small ("infinitesimal") spacetime region, one can always find a reference frame - an infinitely small elevator cabin, observed over an infinitely brief period of time - in which the laws of physics are the same as in special relativity. By choosing a suitably small elevator and a suitably brief period of observation, one can keep the difference between the laws of physics in that cabin and those of special relativity arbitrarily small.

(Even this needs the additional qualification that we are only talking about a "first-order" formulation of the laws of physics, see my answer here).

So, I think there is no contradiction because one is about the global view and the other is about the local view. If you view a large region of space over a large period of time, and both the light ray and each individual donut are approaching from far away, getting deflected by the gravitating body and traveling on to some distance far away from it, it may be true that in the asymptotically flat regions, the angle by which the light gets deflected before and after the flyby is twice the angle each individual donut gets deflected before and after the flyby. On the other hand, if the trajectory of each donut intersects with the trajectory of the light ray such that at some moment the light ray passes through the donut's center, it can be true that in a locally inertial frame in a very small spacetime neighborhood of the intersection point, the donut and the light ray both have the same velocity component in a direction that lies in the plane of the donut's circumference. But since each donut's path only intersects the light ray's once, and since they have different total velocities as seen in local inertial frames at the intersection point, there's no reason to expect that from the global perspective the donut will follow the same overall path through space as the light ray.

Answer 2

It would be better to comment this but I only just joined, so no reputation...you'll also have to forgive me if this is a silly idea, I'm not a physicist :), it's just my 2c.

For the sake of argument, assume that (from the perspective of an observer on the "ground") the light deflection really is twice as large as the bagel's rate of fall - or at least different, since otherwise the question is moot. Then the most logical inference, to my mind, is that the contradiction is itself the answer. That is to say...

As Hypnosifl has pointed out, you can't really get the "uniform field" we're imagining in the problem; so while from the bagel's perspective the light bounces back and forth between the mirrors, what an observer on the ground sees it this:

That is, mirrors that are perpendicular to each other from the bagel's perspective are not perpendicular to observer on the ground (because of the gravitational field), they're bent over slightly so that they're perpendicular to the path of the light, and the light bounces back and forth like a tennis ball. Kind of like - the very phenomenon that causes the light to be deflected at twice the rate expected is the same one that causes this, and fixes the contradiction it introduced. So, the observer on the ground sees the light bouncing back and forth as illustrated in the figure, until the bagel and light hit the ground together.

The same kind of reasoning could apply to the variant with lots of bagels in a row. The bagels see themselves in a straight line with the light travelling straight through their centres; but an observer on the ground sees the bagels lying on a curve that accounts for half of the deflection of the light. When dropped, the observer sees the bagels all fall together, and the light going through all their centres - the extra deflection being accounted for by the fact that the bagels aren't in a straight line from his perspective.

Again, I'm not a physicist so I may have missed some important points (both here and in reading the first answer), but hopefully this makes a little sense.

Answer 3

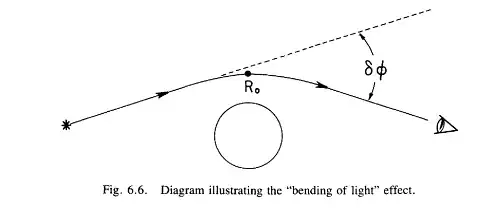
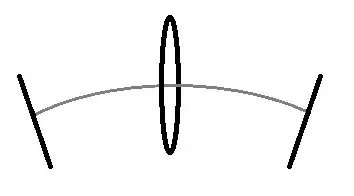
The laser goes through the bagel hole each time until it hits the ground (assuming the mirrors are set up nicely orthogonal to your uniform gravitational field).

To see why, the equivalence principle is all we need. You can imagine thrusters powering an elevator without gravitational fields, set up your mirrors and do the experiment, and that's what you get.

But what about the doubling of the deflection? Einstein originally used the equivalence principle alone to predict a deflection of light that was half what he predicted later using full General Relatvity. I just used the equivalence principle alone. Did I repeat a mistake? No. Einstein's original calculation neglected the spatial curvature, specifically the fact that the curvature was different from place to place. So Einstein's original calculation is exactly what we need for your uniform field situation!

The bounty was for well-cited answers. Mathpages is accessible. You can pick up a textbook on General Relativity, such as Chapter 18 of Schutz’s Gravity from the Ground Up (which is historical and modern and practical and both algebra and calculus based if I recall correctly) or chapter seven of Clifford Will's Theory and Experiment in Gravitational Physics. And here is a review of Einstein's Review article of 1916 (the one where Einstein correctly predicted the deflection) Review of Albert Einstein's 1916 Review Article on General Relativity

So that's the answer, the reason, and citations. But I also want an answer to be maximally educational, so let's put everything in a proper perspective.

General Relativity has a Newtonian Limit. In that limit it is the time-time part of the curved metric that gives the biggest effect (and the only surviving effect if all the otehr effects get smaller and smaller enough which happens in an extreme newtonian limit). The newtonian limit happens far from compact sources, it happens also at low speeds (we are trying to get newtonian here), and you need both the weak gravity and the slow motion to get the newtonian limit. Historically this is originally what Einstein was computing because he was finding the effect of the time-time part of the curved metric from the equivalence principle.

Now, sometimes the newtonian limit doesn't hold, there could be strong fields (large rotation, nearby compact mass, etc.), there could be fast motion. Light is always fast, there is no way around it. So you can't use the newtonian limit for light, and the variation of the spatial curvature then becomes important. When Einstein took that into account, that's when he got the twice the deflection result.

So to summarize:

1) In a uniform weak field, the equivalence principle is fine, gravity and acceleration are basically the same.

2) The newtonian limit is based on the curvature of time, not of space.

3) When there is spatial variation of the curvature that can't be ignored (such as a nonuniform field and fast motion), then other curvature (such as spatial curvature and its variation) matter.

4) A strong field can be strange too, there can even be strange effects, like an Unruh effect making a Geiger counter tick in empty space when accelerated by an elevator. (I'm not sure if that's been observed, but I just wanted to say that strong fields can be important too)

So in a nonuniform field such as the sun, a very fast particle also needs to take variation of spatial curvature into account, it's not just an effect for light. In a uniform field, there isn't anything to take into account, so no extra deflection for light or for fast particles. And those effects are about variation of the curvature from place to place, so they strictly go beyond the equivalence principle which is about small enough regions that you ignore variations, if you have to take those variations into account, then you need more than just the equivalence principle. The additional deflection from the variation is an effect in addition to the equivalence principle. And there are many competitors to General Relativity that have an equivalence principle but disagree on the additional deflection (see Clifford Will's book), so it's definitely a real thing. It's just not a thing you have to worry about in a uniform field.

Answer 4

… photons undergo twice the deflection from gravitational fields as do physical objects.

I don't think this is a correct assessment of the situation. Rather, there is a Newtonian way to predict the deflection of light due to gravity: assume that the light is made of corpuscles with effective mass $m=E/c^2$ which enter the gravitational well with speed $c$ and accelerate under the influence of gravity. Consider this nice animation (possibly by Edward Wright of UCLA) comparing the undeflected, Newtonian-deflected, and GR-deflected paths for light:

Notice, if you look closely, that the red "Newton" photon reaches the observer before the black undeflected photon — a clear violation of the non-Newtonian constraint that light always travels at or below $c$.

The Newtonian path isn't followed by "physical objects," as if photons were "mystical objects" subject to different rules. The Newtonian path isn't followed by any objects, because Newtonian physics is wrong for objects with speeds near $c$. Any physical object with $mc^2 \ll pc$ will follow the relativistic path, including zero-mass objects like photons.

For your bagel experiment, set the mirrors parallel to the bagel's fall path (rather than parallel to local plumb lines) and the reflected laser pulse will stay in the bagel's hole all the way to the core of the earth. The equivalence principle wins.