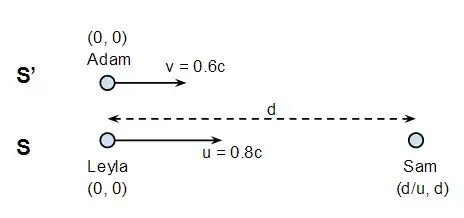Lorentz transformation paradox

Question

I got to solve a simple exercise about special relativity when I kinda came to the conclusion it doesn't stroke with my intuition.

The homework-problem

The problem was about two people Sam and Leyla in a reference frame $S'$ that moves to the right relative to another reference frame $S$ at rest with a speed of $0.6c$ ($c = $ lightspeed). Now another person Adam looks from reference frame $S$ to Sam and Layla who are standing $1.8 \cdot 10^{12}$m apart and throwing a ball (Leyla throws to Sam) at a speed of $0.8c$ in the opposite direction of the movement of the reference frame $S'$ they're in (so actually $-0.8c$).

I already calculated several things. So I know the distance for Adam in reference frame $S$ is $1.44 \cdot 10^{12}$m and the speed of the ball is $0.385c$. Both time dilatation and Lorentz transformations got involved for these calculations.

The question that's causing the real trouble

Now I have to calculate the time needed for the ball to reach Sam (who is standing left to catch the ball) in the eyes of Adam.

I kind of thought the time difference could be calculated with time dilation, knowing that the time difference in $S'$ is $7500$s, but this doesn't lead to the correct solution (result was 9,375s). I also tried calculating the time difference with the fact that I know the speed of the ball and the distance relative to Adam, but this doesn't give the correct result either (result was 12,468s) and this is where my intuition breaks because this means the ball seems to need less time to reach Sam than the time it needs to cross $1.44 \cdot 10^{12}$m if it has a speed of $0.385c$.

The correct answer should be 4,875s and can be calculated with Lorentz-transformations.

My specific question

Why should this be the only correct answer and what are the mistakes in my reasonings, please?

Answer 1

So I know the distance for Adam in reference frame S is 1.44⋅1012m and the speed of the ball is 0.385c

This is true.

this is where my intuition breaks because this means the ball seems to need less time to reach Sam than the time it needs to cross 1.44⋅1012m if it has a speed of 0.385c.

It doesn't have to cross $1.44 \cdot 10^{12}\; \mathrm{m}$ according to Adam.

Remember, according to Adam, during the time the ball is travelling leftward at $0.385c$, Sam is travelling rightward at $0.6c$; the ball does not travel the entire initial separation distance before reaching Sam.

One need only set up the relation

$$\left(0.6 + 0.385\right) c\Delta t = 1.44 \cdot 10^{12}\; \mathrm{m}$$

to find the time of flight according to Adam to be

$$\Delta t = 4875\; \mathrm s$$

---

but why is the time dilatation formula not valid in this case?

The time dilation formula is valid in this case if one applies it properly. The time dilation formula relates coordinate time to proper time (the elapsed time according to a single clock).

In this case, the relevant proper time is the elapsed time according to the ball's clock. This is an invariant, i.e., Adam, Sam, and Leyla agree on the elapsed time according to the ball.

According to the time dilation formula, the elapsed time according to the ball's clock is

$$\Delta \tau = \frac{\Delta t}{\gamma_v}$$

Since $\Delta \tau$ is invariant, we then have

$$\frac{\Delta t'}{\gamma_{0.8c}} = \Delta \tau = \frac{\Delta t}{\gamma_{0.385c}}$$

or

$$\Delta t = \frac{\gamma_{0.385c}}{\gamma_{0.8c}}\Delta t' = \frac{1.0835}{1.6667}7500 \; \mathrm s = 4875\; \mathrm s$$

time dilation states that clocks in moving reference frames should run slower and thus measure shorter intervals

That's correct; if one calculates the elapsed time according to the ball, it is indeed less than either elapsed coordinate time:

$$\Delta \tau = 4500 \; \mathrm s$$

Answer 2

I see you have accepted Alfred's answer, but for the record it is very risky to answer questions like this (especially in an exam) by using the time dilation/length contraction formulae and waving factors of $\gamma$ around. The way the examiner will be expecting you to do it is to use the Lorentz transformations, and the question will usually have been designed with that in mind.

In this case the first step is to draw the geometry in the rest frame of Layla and Sam. It looks like:

We are taking Layla and Sam's frame as the rest frame so I've called this $S$. In this frame Layla and Sam are separated by a distance $d$ ($1.8 \times 10^{12}$m) and Layla throws the ball with a velocity $u$ ($0.8c$). So the ball reaches Sam at $(t = d/u, x = d)$. To answer the question we just transform these two events into Adam's frame $S'$.

As per usual we make life easy by choosing our coordinates so the origins coincide when Adam passes Layla, and we can wihout loss of generality take this as the moment Layla throws the ball. So the ball is thrown at the spacetime point $(0, 0)$ in $S$ and $S'$.

Now we transform the point $(d/u, d)$ from $S$ to $S'$. Actually we only need $t'$ because the question is when Sam catches the ball, not where. So we just plug our numbers into the Lorentz transformation for time:

$$\begin{align} t' &= \gamma \left( t - \frac{vx}{c^2} \right) \\ &= \gamma \left( \frac{d}{u} - \frac{vd}{c^2} \right) \end{align}$$

Just plug in the values for $u$, $d$ and $v$, and you'll find the result is 4875 seconds.

I can't emphasise enough how dangerous it is to use the time dilation formula unless you really understand what you're doing. It's alright for experienced physicists like Alfred, but no-one starts out that way, and your confusion with Alfred's answer illustrates my point. By contrast, using the Lorentz transformations as I've demonstrated is unambiguous and straightforward. The only hard bit is being clear about what events you need to choose.

Sermon over!