Does a moving magnetic field produce an electric field?

Question

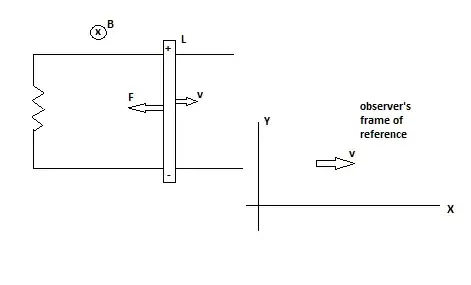
Consider a conducting rod of length $L$ moving with speed $v$ in a magnetic field of intensity $B$. Let all the three parameters be perpendicular to each other. Moving charges in a magnetic field experience a force, which will be in the downward direction in this case. This will cause the electrons to accumulate towards lower end of the rod, thus causing a difference in potential. We know that the emf induced in the rod will be $E=BLv$ or $\vec E=\vec B.(\vec L\;\mathrm x\; \vec v)$ to be more precise. Thus, a current is induced in the rod. A current carrying conductor placed in a magnetic field experiences a force, whose magnitude is given by $F=IlB$ in the direction opposite to that of the velocity of the rod.

Now, consider an observer moving with the same velocity as that of the rod. For him, the charges are stationary. Yet, the rod experiences a force. Now, as far as I know, the only thing that can cause a force on stationary charges is an electric field. So, for him, there must exist an electric field in the direction same as that of velocity of rod, which is causing the electrons to experience a force in the opposite direction (electrons are negatively charged, so force will be in the opposite direction to that of electric feld).

So, does a moving magnetic field produce an electric field?

Answer 1

Yes. Faraday's law of induction is $$\nabla\times\vec E=-\frac{\partial \vec B}{\partial t}$$ A moving magnetic field thus produces an electric field.

Answer 2

Formally, the fields don't actually move, they propagate. The fields are defined as a function of space and time: $$ \mathbf B=\mathbf B\left(t,\,\mathbf x\right) $$ Only when $\mathbf B$ is constant in time do we call it a static/constant field.

Maxwell's equations tell us, in differential form, that a time-varying magnetic field produces an electric field and a time-varying electric field produces a magnetic field: \begin{align} \frac{\partial\mathbf B}{\partial t}&=-\nabla\times\mathbf E\\ \frac{\partial\mathbf E}{\partial t}&=\frac1{\epsilon_0}\nabla\times\mathbf B-\frac{\mu_0}{\epsilon_0}\mathbf J \end{align} where $\mathbf J$ is the current density.

In relativity, the two fields actually comprise the electromagnetic field tensor, $$ F^{\mu\nu}=\left( \begin{array}{cccc} 0&-E_x/c&-E_y/c&-E_z/c \\ E_x/c & 0 &-B_z & B_y \\ E_y/c & B_z & 0 & -B_x \\ E_z/c & -B_y & B_z &0 \end{array}\right) $$ Which really means that that are the same thing. See also

• Does special relativity make magnetic fields irrelevant?
• How do moving charges produce magnetic fields?

Answer 3

For that problem the speed of the rod is not constant then you would never see the rod stationary so you will always have a change in the magnetic flux and by Faraday's law of induction an emf.