3

I have found these notes: http://www.physics.usu.edu/Wheeler/QuantumMechanics/QMWignerEckartTheorem.pdf

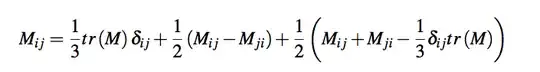
Which state on page two that a matrix (M) can be broken up into rotationally independent pieces like so: enter image description here

(ps: I believe the last term should have 2/3 and not 1/3 in front of the delta_ij, but please tell me if I am wrong).

My question is: why is it that a matrix can be broken up into these three parts? Is it always these three parts (trace, symmetric, and anti-symmetric parts)? I am new to the concept of irreducible tensors and I think this relates to them.

I have tried reading previous threads about this on here: Irreducible tensors concept and here: Irreducible decomposition of higher order tensors however, none answer the question of why it is even possible to break up a matrix like so. Where does this concept come from?

Community
  • 1
Guest
  • 375

2 Answers2

4

An order-2 tensor is usually decomposed in that way because each part behaves differently under a certain symmetry. For example, if the symmetry is just rotation, then the term with the trace transforms like a scalar; the anti-symmetric part $M_{ij}-M_{ji}$ of the tensor transforms like a pseudo-vector, while the traceless symmetric part (the last term) transforms like an ordinary 2-tensor.

Phoenix87
  • 9,759
0

They can be broken up in many ways, it's like choosing a base for a vectorial system, however in physics the symmetries play an important role, that's why we use this system to reduce tensors, because it contains physical information. The matrix can be broken into these three parts and in other ways too, this is just the most convenient.

And yes, it is a factor $\frac{2}{3}$ in the second $\delta$.

manuel91
  • 336