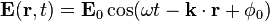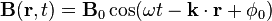We can explain conservation of energy in interference phenomena by saying that there is redistribution of energy. However if only 2 photons in opposite phase "combine" then how can we explain conservation of energy?
Could it be that if we think from wave view-point then we'll find nothing and if we think from particle view-point then there will be 2 photons?
Experiments in which we see fringes, are usually of "single particle interference" (single photon in your case). What interferes is not two photons. For an example, consider a single photon wave reflected at a mirror and producing interference near the mirror. What interferes is not 2 photons, but the direct part and the reflected part of the same 1 photon wave.
Now, some clarification (maybe for future question marks). Usually, in order to obtain a long region with fringes, what we call 1 photon is actually a coherent beam with very low average number of photons. Such a beam may be very long. (If you didn't learn yet of coherent beams, then imagine a laser beam, though very, very weak s.t. if we detect it we find 1 single photon.)
I didn't say that there don't exist beams of two photons that can travel together as a single particle - they are named do-photon. But they are more complicated, and it doesn't seem that you refer to them.
So, bottom line, the interference phenomenon has the best treatment in the wave-language. The particle-language is more suitable for other type of experiments.
The phase of a photon is not the phase of the electromagnetic wave it helps build. In the electromagnetic wave the phase describes the electric and magnetic fields
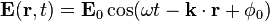
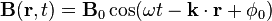
t is time (in seconds),
ω is the angular frequency (in radians per second),
k = (kx, ky, kz) is the wave vector (in radians per meter), and
phi_0 is the phase angle (in radians).
A photon is an elementary particle of spin one, either along its direction of motion or against it. The electromagnetic wave is composed of an enormous number of photons.The fields of the EM wave are built up by these photons. Each photon has its quantum mechanical wave function : its location in space and time is given by a probability distribution. In a coherent build up of the classical wave the macroscopic phases will appear, but the way an individual photon's wave function contributes to the macroscopic phase is complicated. In this link there exists a discussion of how the classical wave emerges from the quantum state of the photons.
With the above in mind, that the photons are not described by the classical EM wave phase:
However if only 2 photons in opposite phase "combine" then how can we explain conservation of energy?
when we have two photons we do not have a beam of light carrying energy, we have two elementary particles which can only interact very weakly through higher order diagrams. . Each photon will be carrying the energy $E=h\nu$ and there is no problem with conservation of energy.
If we have a beam of light falling on two slits, we will see an interference phenomenon, and this interference is seen in the energy carried by the beam and impinging on the screen.
If we send individual photons at a time, we will see individual spots on the screen, depositing their energy; it is the accumulation which will show the interference pattern of the wave.
Could it be that if we think from wave view-point then we'll find nothing and if we think from particle view-point then there will be 2 photons?
It is not a matter of thought. There will always be the energy of the individual photon, in macroscopic interference it is just deflected according to the probability distributions for the particular quantum mechanical problem, which happen to coincide with the macroscopic interference patterns. This is not surprising because, if you read the link, it is the Maxwell equation that enters in both classical and quantum cases, with different mathematics.
C'est justement un problème ? ou passe l'énergie si les deux quanta dénergie sont opposé en phase et en amplitude ? . Soit c'est impossible a réalisé pour des raison quantique ou soit c'est possible et dans se cas la, avec les franges d'intérférence des champ électromagnétique il parait que le bilan dans les zones éclairé compensent les pertes dans les zones sombre donc il y a un transfert d'énergie . Dans le cas des deux photons ou l'énergie est transféré ? dans le vide probablement . Je pense que les deux photon réel vont produire une particule et antiparticule du vide qui pevent étre associé a des photons virtuel donc une conversion de particule réel en virtuel . L'énergie serait alors à deux composante ? probablement puisqu'il faut justifié le potentiel d'énergie de la force de casimir ou autre phenomènes paranormaux avec une théorie avancé qui doit faire la jonction avec les intéractions électromagnétiques dans le vide à cause des pertes d'amplitude de la lumière en lien avec l'impédance .
Conclusion : Il faut une théorie de vide et c'est déja fait mais elle reste au niveau post doctorant à se qu'il parait .
