The electric field in wires in a circuit

Question

How is the electric field maintained throughout the wiring / the conductors from component to component? The charges are moving far away from the voltage source (the battery) so how is the electric field maintained?

A very simple example

A very simple example is two capacitor plates charged. There is postive charge on one and negative on another plate. This gives a uniform electric field between them with high potential at the positive plate and lower potential at the negative.

• If a straight wire is placed between the plates without touching, charges will move in the wire (for a very short while, I know) from higher to lover potential.

• If a not-straight wire is curving away (maybe into other parts of the circuit) and away from the space between the capacitors, then the charges in the wire are not inside the electric field the whole time.

So what is moving them? There must be an electric field throughout the wire all the way, to cause a force on the charges to keep them moving, but how is it created?

Answer 1

There is a portion of that wire near the plate with the positive charge, in that portion of the wire, conduction electrons will want to flow towards it. But each conduction electron then leaves behind a excess of positive charge because the proton it used to cancel out no isn't cancelled out, so a conduction electron a bit farther away is attracted to the proton location vacated by that electron.

It's like a job market. You can hire away a best employee from another firm, then that firm, who used to have the best because they wanted the best now replaces that person with the second best employee by stealing them from another firm, and now that firm has to steal the third best from another firm, etc.

In short that constant electric field is just the electric field due to the plate capacitor, but every proton and electron in the wire also produces its own electric field and the electrons in the wire respond to the total field, even the fields due to the other electrons and protons in the wire.

Answer 2

Resistive materials in your capacitor dielectric will totally distort the field pattern and essentially "guide" the e-field so it extends outside the plates.

Therefore we must make changes to clarify things. First, replace your wire with a large number of hundredth-ohm resistors in series. Mark the voltages at each node, then sketch in the field lines. You'll find that the chain of resistors is acting like a "hose for e-field" as well as a hose for current. Inside the resistors, the field lines are directed axially along the path of current. And just outside the resistors, the field lines are roughly the same as inside.

So in your diagram, the wire is forcing the e-field to "flow" parallel to the wire, so it extends far outside the plates, then goes back in again.

More detail: since wires are conductive, then in the steady state there cannot be net-charge inside the material. Instead, net charge appears on the surface of the wire, and takes the form of rings of various charge-densities. A wire becomes a stack of rings of surface charge, with positive rings on one end, negative on the other, and a continuous axial e-field inside, with the field lines parallel to the wire.

Note that if your wire is a perfect conductor, then none of this applies, and there is no voltage-drop along it, and no e-field within. Only real, resistive wires require an e-field to drive the charge-flow.

Your question is extensively answered by the authors of the physics textbook "Matter and Interactions," in their pdf preprint:

A unified treatment of electrostatics and circuits, Chabay and Sherwood, 1999

Answer 3

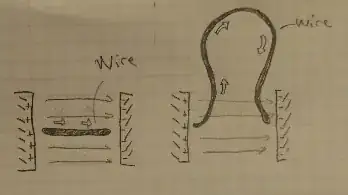
When you insert a third conductor between two plates of a capacitor, you essentially create a three-plate capacitor.

The usual way to obtain the static solution (capacitors with general arrangements of the plates) to such problems is to assume the conductive materials are ideal conductors and use a numerical method such as finite elements to solve Poisson's equation for the fields in the dielectric region. Then, we obtain the charge on the surface of the conductors from the electric flux terminating on the conductor. Since we have assumed ideal conductors we know that in the static case all charge must be on the surfaces, and the field is infinitesimal (or else charge would be flowing and the solution would not be static).

If a not-straight wire is curving away (maybe into other parts of the circuit) and away from the space between the capacitors, then the charges in the wire are not inside the electric field the whole time.

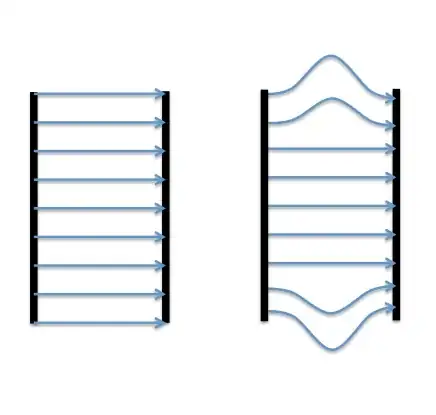
Remember that the solution giving uniform E field between the capacitor plates depends on the plates being infinite in extent. So it's not possible for the wire to extend beyond the influence of the plates in this situation.

If we want to know the field distribution for non-infinite plates with a conductive material imposed between them, we again have the three-plate capacitor problem with arbitrary geometry, for which there aren't general solutions, but which we can solve numerically.

So what is moving them? There must be an electric field throughout the wire all the way, to cause a force on the charges to keep them moving, but how is it created?

If we assume an ideal conductor, it only takes an infinitesimal field to cause a large current to flow. In a real conductor there will be a nonzero field until the charges re-distribute. Once the static situation is reached, the fields produced by the surface charges will balance whatever imposed fields are present and the net field within the conductor will be zero.

Determining the fields during the initial charge flow will again probably require a numerical solution. In any real situation where this flow matters, the light speed limitation on the propagation of the fields in the dielectric is likely to be at least as important as the resistance of the material, so a full electromagnetic wave solution will probably be required.

Again, we'd solve for the electric and magnetic fields, and use the field solutions to infer the charge distribution.

Answer 4

Wen you look at the electric field of a parallel plate capacitor with finite size plates, then you have to consider the shape of the field at the edge. It's more like the diagram on the right than the diagram on the left:

What this means is that as the wire leaves the parallel plate capacitor, it doesn't suddenly "step out" of the field.

Secondly, the forces on the charges in the wire (induced by the electric field) cause an internal polarization - the positive and negative charges will separate just far enough so that the field they generate internally exactly cancels out the parallel component of the external field at each point of the wire. So where the external field (parallel to the wire) is large, the internal polarization will be large - where the external field is small, the polarization will be small. And it's the integral (sum) of all the polarization along the wire that describes the total charge splitting.

In other words - when charge is moved, it has to "go somewhere" and it leaves behind the opposite charge (a neutral conductor must contain equal amounts of positive and negative charges; current flows when these charges move relative to each other).