1

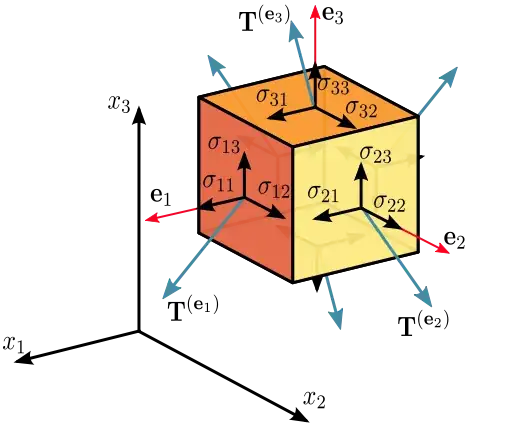
I have a couple of questions related to the diagram in the answer by Kyle Kanos to this question, Why is stress a tensor quantity?.

Q1. If the box shown is of finite size why are there not three force components on each of the six faces?

Q2. What happens to the stress tensor when the box shrinks to a point?

Response to Answer by Kyle Kanos

Thanks for the answer but I think I need to clarify Q1 because the answer does not seem to be an answer to the question I intended. Each of the six faces of a finite size box will in general have a different net force acting on it and each net force can be resolved into three orthogonal components. Therefore why doesn't the stress tensor have (6 faces) x (3 orthogonal components) = 18 components?

Community
  • 1
gjh
  • 11

1 Answers1

2

  1. Technically, no force was labeled, it was only stresses, $T,\,\sigma$, and unit vectors, $\mathbf e_i$. But note that there totally are 3 sets of $\sigma$ arrows on each face! See:
    enter image description here
    They're not actually labeled, but they're definitely there (just hidden). Since there are only three orthogonal directions here, $\hat{\mathbf{x}},\,\hat{\mathbf y},\,\hat{\mathbf z}$, there can only be 3$\times$3 components: \begin{align} \mathbf T^{e_1}&=T^{e_1}_1\hat{\mathbf x}+T^{e_1}_2\hat{\mathbf y}+T^{e_1}_3\hat{\mathbf z}\\ \mathbf T^{e_2}&=T^{e_2}_1\hat{\mathbf x}+T^{e_2}_2\hat{\mathbf y}+T^{e_2}_3\hat{\mathbf z}\\ \mathbf T^{e_3}&=T^{e_3}_1\hat{\mathbf x}+T^{e_3}_2\hat{\mathbf y}+T^{e_3}_3\hat{\mathbf z} \end{align} which gives us the 9 components.

  2. I suppose I'd argue that nothing happens to the stress tensor, it stays what it is (well, defined as it is). What happens is the surface area, $dA$ becomes zero and $T\,dA=0$ which means that the force on the surface is zero (i.e., the point cannot deform).

Kyle Kanos
  • 29,127