In reverse time, do objects at rest fall upwards?

Question

I want to develop a game where time runs backwards, based on the idea that physical laws are reversible in time. However, when I have objects at rest on the earth, having gravity run backwards would mean that the objects are repulsed and falling upwards. Obviously, that is not how things happen in the real world (objects stay at rest for a long time without having just fallen down) so what is my logic mistake? How can I start planning a simple physics engine with a reverse time flow with gravity without that happening?

Answer 1

The direction of the gravitational force would not change under time reversal. Your object would feel a force downward, just as it does usually.

It might be easier to imagine you had a movie of an object under the influence of gravity. Drop the ball from rest some distance above the floor. You'll see it move downward and speed up. You'd interpret this as a gravitational force downward.

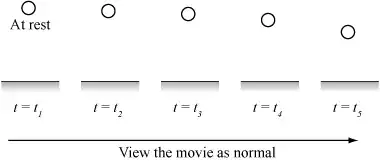
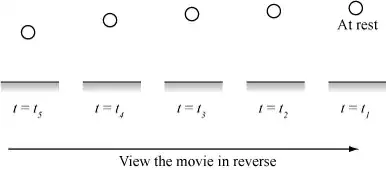
Then, upon playing the movie in reverse, you'll see the ball move upward with decreasing speed. This observation is still consistent with a gravitational force downward.

Answer 2

There is no mistake. The laws of physics themselves are reversible in time, but the solutions not necessarily so. Thus, the "behavior" of the universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics. The second law is about the behavior of the solutions, is not a fundamental law in itself. In your specific example of the object being "repulsed" when the movie is running backwards, the physical reason is not that gravity becomes repulsive. Gravity will still be attractive. The reason why the object moves back upwards is the unlikely chance (due to the second law) that the motion of the molecules on the floor, air, and electromagnetic radiation coordinate, by chance, to push the object up (the reversal of what happens when a non-elastic object hits the ground). That is, the energy of the system, which is spread out into many particles, gets back together into a macroscopic object, a very unlikely event (but one that does not violate the laws of physics. Of course, this would be the cause in the physical world where the laws are time symmetric. In your simulation, which is not made up to microscopic detail, the reason is that the laws themselves are irreversible (the way you implemented the code).

For more details, see here and here.

Answer 3

One of the problems you will encounter is causality.

Imagine you have a ball resting on the ground.

Without already knowing how it behaved in the past you cannot uniquely define the next frame of your game. You cannot tell if the ball should:

• move upwards vertically.
• move upwards in any direction.
• roll on the ground towards any direction.
• do nothing.

You could use it as a part of your game design to decide which one of the above it should be.

Note that if for instance you decide that the ball must move upwards at the speed of 40 m.s^-1 in the next frame, then in the consecutive frames it must keep its direction and have a position/speed consistent with the acceleration (deceleration in reverse time) so that after 1 sec, the speed of the ball is 40 - 9.81 = 30.19 m.s^-1. Integrate speed for position in each frame.

Answer 4

Imagine a flowerpot sitting on a ledge. A breeze blows the pot off of the ledge, and it falls to the ground. When it hits the ground it shatters into a bunch of pieces, it kicks up dust, it makes a sound, it vibrates the ground, and the shards come to rest.

The time-reversal of this is that some pieces of flowerpot are sitting on the ground. Suddenly a cloud of dust, along with vibrations in the air and ground, coalesce underneath the pot shards with such precise timing that the shards are kicked into the air. On the way up, they align themselves in the right shape, and cold-weld together to form a seamless pot. The assembled pot traces an arc up to the ledge, where the breeze (blowing in the opposite direction) sets it down gently.

This is an incredibly unlikely scenario, but completely compatible with the laws of physics (and un-reversed gravity). The nature of the arrow of time is that large-scale forward processes tend to dissipate energy and increase entropy, while "reversed" processes involve highly unlikely coincidences that concentrate energy and decrease entropy. Ultimately it is believed that we can trace this to the fact that the universe just after the big bang had a much lower entropy than it theoretically could have, and ever since then it's been moving towards a higher equilibrium entropy.

Answer 5

To make such a game and have it make sense, you would have to use a much simpler physical system than anything you would reasonably encounter on Earth's atmosphere. For heat-dissipating systems, the laws of thermodynamics give time a direction: the direction of increasing entropy. Thus an object that falls to earth dissipates its energy, mostly as heat. You never see that heat spontaneously coalesce out of the environment to fire the object back into the air. On the other hand, if the object didn't dissipate its energy, it would bounce forever and the system would look exactly the same moving forwards or backwards in time. Note in both cases that gravity still points down, as BMS said.

Answer 6

In reverse time, it would seem gravity is still attractive. But the quick impulse force that stopped the motion of something falling would instead send it upward at some inital velocity, which gets slowed by gravity.

Otherwise, the object would accelerate from rest away from earth. My hunch would be that all conservative force fields remain the same regardless of the arrow of time.

Answer 7

For the limited context of Newtonian mechanics, I will provide you with an insight non demostrative:

If you take most problem in mechanics found in a textbook (for example two bodies orbiting each other, and point planet orbiting a large mass unmovable body, or a mass hung from a spring, or a rigid body wheel rolling on a surface (this one is more theoretically complicated)), and given the initial conditions (position and velocities of all relevant masses involved) at time t0 (the velocities) and the forces wich give the equations of motion, if you solve and find a unique solution for the motion of the bodies involved , you can actually do this and it works.

Take a time t1>t0 and take note of the "initial conditions" there (we call them "final conditions"), Invert the sign of the velocities of final conditions, but mantain their positions, and if you call this new "initial conditions 2", if you now solve for the exact same forces, with "initial conditions 2" as the initial input, you will find that the unique solution is the movie played backwards of the previous solution found, and that at t0 effectively the masses "return" to the same spots, and with the velocities, only the sign changed.

One way to understand this is that if you "record with a camera" the movie of the original solution, and play it backwards, it's very intuitive that, comparing the movies at the correspondent moments: -The positions of the masses match exactly. -The velocities have exact opposite sign. -The acceleration matches exactly.

Because each time you derive you are multiplyng for a minus sign, because time is at the "wrong way". Velocities get a minus sign and then acceleration is velocities with a new minus sign, so it gets to be the same.

That means that if acceleration is the same at the same moment, and position is the same, since Newton equations don't normally depend on velocities (AND WHEN THEY DO THIS WHOLE ANSWER IS INVALID, IF FORCES DEPEND ON VELOCITY LIKE friction with air, then take more care ) then newton equations with the same force definition must be true. That's why when solving you get the bacwards movie exactly.

Answer 8

Proporties that are independent of time will not change when time is reversed, forwards or backwards, or changed in any other way.

Anything dependent of time will run backwards.

In general we may say that any change of any proporty (causing a difference $\delta f(t)$ over a time difference $\delta t$ between "before" $t_{1}$ and "now" $t_{2}$, that is $\frac{\delta f(t)}{\delta t} \neq 0$) will be reversed. As in a movie played backwards.

Answer 9

In Reverse Time, objects would experience a inversion of velocities and accelerations. Instead of a falling ball moving toward the ground and gaining velocity, it would be moving away from the floor and losing velocity. When it returned to the spot it was dropped, its velocity should equal 0.

To achieve this, change the sign on it's velocity along the vertical axis, and apply a constant acceleration of anti-gravity (-9.81 m/s2). Other forces would have to be inverted also, so a bullet traveling 250 m/s along an x-axis and accelerating at -2 m/s2 would travel at -250m/s (negative means the opposite direction) and accelerate at 2m/s2. Until it got back to the barrel of the gun.......

Answer 10

In a physics sense, the acceleration would still be downward (time is squared in acceleration, so reversing time doesn't make the square negative), but it's the second law of thermodynamics that's really being reversed.

Instead of getting nudged off of a table, falling to the ground, and bouncing succesively smaller bounces, a ball would be shot from the ground, bounce higher and higher, and finally land on the table.

So in your game, make things spontaniously get jolted from the earth, and gain more energy every time they hit the ground, until they land on something higher up.

Answer 11

Your logical error: you are confusing the direction of time and the direction of entropy.

Elementary physical processes may be time-reversible. Complex processes are (nearly!) never reversible, due to the second law of thermodynamics.

So your game should be about elementary processes. Also (simplified) models may be time reversible in your game, for example a model of the solar system.