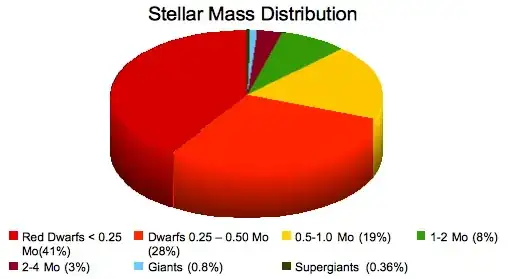
The answer is that 41% of the stars have masses below 0.25$M_{\odot}$.
To check this I integrated the Kroupa initial mass function. This is that $N(m)$ the number of stars per unit mass is proportional to $m^{-1.3}$ for $0.08<m/M_{\odot}<0.5$ and proportional to $m^{-2.3}$ for higher masses.
If I integrate this I find that the ratio of stars with 0.08-0.25$M_{\odot}$ to those with 0.25-0.5$M_{\odot}$ to those with 0.5-1$M_{\odot}$ is 3.64:1.68:1 - which is roughly consistent with the pie chart, where the ratios are 2.15:1.47:1 The differences might be explained by a slightly different lower mass limit for the lowest mass bin, or perhaps a different IMF.
On the other hand if I integrate $mN(m)$ over the same limits I get a ratio of mass contained within stars between these limits in the ratios 0.78:0.89:1 which is clearly inconsistent.
The comparison at higher masses is dependent on what is assumed for the star formation rate - i.e. you need to account for evolution and use the present day mass function rather than the initial mass function.