Confusion about Length Contraction (ex in Muon decay)

Question

I am a bit confused about the implications of length contractions;

For example, in the muon decay problem, we assume that the distance between the muon and the earth is contracted only in the frame of reference of the muon (I've heard justification saying this is because it is Earth's atmosphere) but suppose there were no atmosphere then in the reference frame of Earth shouldn't the length between them also be contracted?

What I don't get is if one object is moving at a speed relative to another object, shouldn't this movement affect the distance between them in the reference frames of both of them, since their movement is merely relative?

Answer 1

Don't confuse time dilation and length contraction,(even if length contraction is a consequence of time dilation) because there is no length contraction for the distance between two reference frames. The length (or distance) must be found in one reference frame, and the observer must be in another reference frame, he may not be part of the reference frame of the distance.

By consequence, it is not the distance between muon and Earth which is contracted. It is the distance between the starting point A of the muon and Earth (if we suppose that the muon is traveling from A to Earth).

From the Earth frame the distance A-Earth is at its largest. For the muon frame, the distance A-Earth is contracting according to its relative velocity.

The example of David Z is the opposite example: There is a distance in the muons' frame (between two muons which are belonging to the same frame) which is observed from the Earth frame.

Answer 2

Length is contracted the other way, we just don't notice it because muons are pointlike particles (as far as anyone knows), and a length of zero is still zero no matter how much you contract it.

If you had a beam of muons spaced a fixed distance apart (and yet somehow their "decay counters" only start at $50\text{ km}$ altitude), then it would be a different story. You could tell that length is contracted by looking at the spacing between consecutive muons. Suppose the muons are traveling at $0.99995c$, so $\gamma \approx 100$. Then, in the muons' rest frame:

• they are spaced, say, $10\text{ km}$ apart
• they take $2.2\ \mathrm{\mu s}$ to decay
• an atmosphere of thickness $50\text{ km}/\gamma = 500\text{ m}$ is approaching them
• that atmosphere will pass by them in $500\text{ m}/(0.99995c) = 1.67\ \mathrm{\mu s}$
• the atmosphere will reach a new muon every $10\text{ km}/(0.99995c) = 33.4\ \mathrm{\mu s}$

In the Earth's rest frame:

• the muons are spaced $10\text{ km}/\gamma = 100\text{ m}$ apart
• they take $2.2\ \mathrm{\mu s}\times \gamma = 220\ \mathrm{\mu s}$ to decay
• they are approaching an atmosphere of thickness $50\text{ km}$
• they will pass through that atmosphere in $50\text{ km}/(0.99995c) = 167\ \mathrm{\mu s}$
• a new muon will hit the atmosphere every $100\text{ m}/(0.99995c) = 0.334\ \mathrm{\mu s}$

You can check that all these numbers are consistent. In particular, in both frames, the muons last long enough to make it through the atmosphere. The time between impacts is shortest in the rest frame of the atmosphere and is dilated by the right factor of $\gamma = 100$ in the rest frame of the muons.

Answer 3

Well, Lorentz transformation and whole special relativity gives us short qualitative answer - time dilation and length contraction are very similar. Sitting on Earth we see muons with slower decay rate, because of time dilatation. Being a muon, we calculate time in our own frame of reference - so to keep calculations clear, we need to contract length instead.

Muon's half life time is 2,2 microseconds. We can assume they travel roughly with the speed of light (0.9997 c). Watching them on Earth, their lifetime is increased, because their clock 'tick tocks' slower. Then if they are, suppose, 660 meters from us, in one second they will reach us.

Okay, but what about being a muon? Our clocks is running with exact speed of rest muon. Then, to reach observer in one second with same velocity, we have to travel shorter distance.

This is why Lorentz contraction and time dilatation are in fact very similar to each other.

Answer 4

Short answer: Yes, length contraction is a symmetric transformation between reference frames. However... You may not like this answer, but I think it's far easier to regard muon decay via the concept of time dilation rather than length of contraction. Reason is, from the standpoint of the muon it's not moving (and yes the Eath is moving but it's not relevant to the muon's decay), and it's going to decay after some time t.

In the earth's frame, that interval of length t gets split up into part time T and part space L, and because of the "minus sign" in the metric it means that the muon seems to 'live longer' before it decays. In units where $c=1$, $$t^2 = T^2 - L^2,$$ so $$T^2 = t^2 + L^2.$$

(If I can figure out how to upload pictures from my iPad I'll show you a couple spacetime diagrams that more directly answer your question re length contraction. Posting what I've got now.)

Answer 5

Confusion about Length Contraction [...] if one object is moving at a speed relative to another object, shouldn't this movement affect [...]

Talk about "length contraction" (or "time dilation") is inherently confusing; it is improper and should be avoided.

In the typical "cosmic ray generated atmospheric muon" example we have the following unambiguous experimental facts:

1. the muon "mean life" duration is $\approx~2.2\times 10^{-6}~\text s$, as it has always been found for samples of "free" muons,

2. the duration of a clock which is (practically) at rest at the bottom of the atmosphere

   • from its indication (practically) simultaneous to the indication of an "air atom" having been hit by a cosmic ray proton and (at the end of a rapid decay chain) having emitted a muon

   • until its indication of being passed by this muon

   is $\approx \frac{1}{\sqrt{ \stackrel{~}{1 - v^2/c^2} }} \times 2.2\times10^{-6}~\text s$.

   From this relation we can determine that "$\text s$" here actually means the same unit duration in both measurements.
   But to call this duration of the clock on the Earth's surface also a "dilated duration of the muon" is plainly a misattribution.

   Likewise:

3. the distance between the described clock and "air atom" is typically $\approx~10~\text{km}$,

4. the distance between the described muon and some (hypothetical) other muon which was "moving behind" at the same velocity (wrt. the clock on the Earth's surface), starting out from an "air atom" which had the same distance ($\approx~10~\text{km}$) from the clock, such that

   • the indication of the former muon having passed the clock was simultaneous to

   • the birth indication of the latter muon

   is $\approx \sqrt{ \stackrel{~}{1 - v^2/c^2} } \times 10~\text{km}$.

   From this relation we can determine that "$\text {km}$" here actually means the same unit distance in both measurements.
   But to call this (thought-experimental) distance between two muons also a "contracted distance between the clock and some particular piece of the atmosphere" is plainly a misattribution.

Answer 6

Useful to add maybe that the apperance of relativistically moving objects can be quite the opposite of length contraction. This is caused by Terrell rotation.

This answer is a substitute for a comment on another answer. But I can't comment yet. It was stated:

If you could see an airplane or a train passing in front of you at relativistic velocity it would appear contracted

It would not necessarily look contracted.

Answer 7

I think most of you are confusing what contracts because of motion. Not the distance between the muon and the Earth, nor the distance between the point in which the muon began its motion and its destination. Length contraction deals with the contraction "of the moving object" (that is the muon's length, if we could talk of it). If you could see an airplane or a train passing in front of you at relativistic velocity it would appear contracted. But the object. And moreover this effect only affects the way you "see" the object (the way it appears to your eyes) not its physical characteristiques, there's no structural deformation. Moving, solid bodies don't become really shorter. This effect is due to the fact that visual information is carried by photons and when the object to be seen has (almost) the same speed of what has to carry the visual information (light, photons) then there will be of course a lack of information, which will be the more greater the more distant the points of that object will be from the observer (photons have no time enough to deliver visual information). So the points at the extremities of the object will be lost when seeing it and the body will appear as contracted. I agree that the case of muons is rather explainable through time dilation.

Answer 8

Introduction

In the initial question, Peter G. Chang asks,

"What I don't get is if one object is moving at a speed relative to another object, shouldn't this movement affect the distance between them in the reference frames of both of them, since their movement is merely relative?"

As far as I can tell, as of the time of writing, none of the six answers thus far submitted address this particular aspect of question.

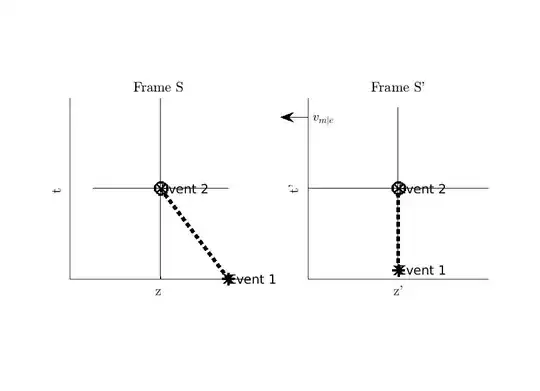
In the figure below I give a standard configuration of reference frames. In both there are two events. One event is the departure of a muon from it time and place of creation. The second is the arrival of the muon to its time and place of colliding with the Earth's surface. There, the left frame is the frame $S$ of the surface of Earth at rest, while the right frame is the frame $S'$ of the muon in in relative motion with respect to Earth. The muon is moving to the left with a speed of magnitude $|-v_{m\mid E}|$.

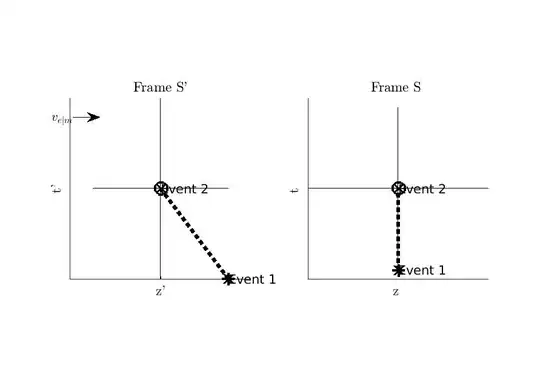
Yet, as indicated by Peter G. Chang, the motion is relative. So, in the figure below I give the standard configuration of reference frames again. In both there are two events. The events are the same as those described in the anterior paragraph. However, the left frame is the frame $S'$ of the surface of Earth in relative motion with respect to muon at rest, while the right frame is the frame $S$ of the muon at rest. The earth is moving to the right with a speed of magnitude $|v_{m\mid E}|$.

Materials and Methods

Materials

We have two objects moving in relative motion with respect to one another. One if a muon and the other is the earth. The relative speed of the two objects as they approach each other is given as $|v_{m\mid e}|= |-v_{e\mid m}|$.

Method

The method is to construct a Minkowski spacetime diagram for both of the standard configuration of reference frames that I give in the introduction.

Results

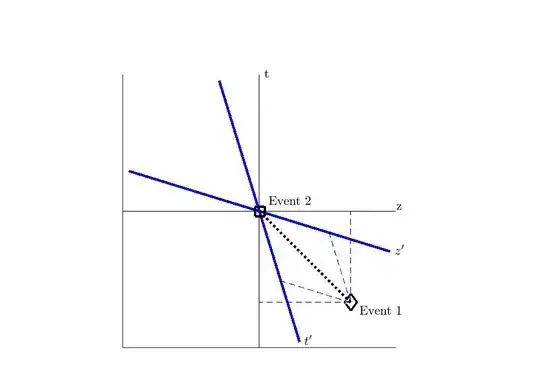
In the figure below, I show the Minkowski spacetime diagram for the first figure in the introduction. Two things are important to note here. First, is that the length that is measured in the frame of the moving muon is contracted with respect to the length that is measured in the frame of the stationary Earth. Second, is that the elapsed time that is measured in the frame of the moving muon is contracted with respect to the elapsed time that is measured in the frame of the stationary Earth. Mathematically speaking, $$ \Delta{t'} < \Delta{t}\qquad \text{and} \qquad \Delta{z'} < \Delta{z}.$$

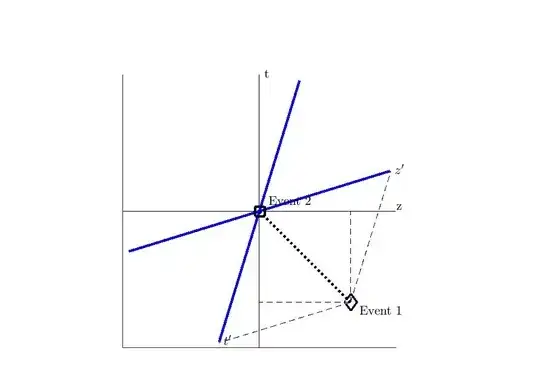
In the figure below, I show the Minkowski spacetime diagram for the second figure in the introduction. Two things are important to note here. First, is that the change in distance that is measured in the frame of the stationary muon is less than the change in distance that is measured in the frame of the moving Earth. Second, is that the elapsed time that is measured in the frame of the stationary muon is less than the elapsed time that is measured in the frame of the moving Earth. Mathematically speaking, $$ \Delta{t} < \Delta{t'}\qquad \text{and} \qquad \Delta{z} < \Delta{z'}.$$

Discussion

Irrespective of how we portray the relative motion (i.e., the muon moving towards the Earth, or the Earth moving to the muon) the elapsed time between the events is measured by a clock attached to the muon is less that the elapsed time between events as measured by a clock attached to the surface of the Earth at the point of collision. Similarly, the spatial distance between the events in the frame of the muon, is less that the distance between the events in the frame of the earth. Either of the two configurations are equally valid to solving this problem, as are each of the two Minkowski spacetime diagrams given in the results.

However, when we solve a problem in special relativity, we have to be careful to equate variables correctly depending on the exact wording in the problem. For example, in 1 Gray writes that "These muons ... are traveling at relativistic speeds with, on average, a $\gamma$ of 40." This indicates that the problem is being specified from the perspective of the first figure in the introduction. Further, Gray writes that, "the muons are created at a nominal height of 15 000 m." Thus, refering to the first figure in the results, we are given $\Delta{t}$ and $\Delta{z}$. From which, we have that $$\Delta{z'} = \frac{\Delta{z}}{\gamma}<\Delta{z} \qquad \text{and}\qquad \Delta{t'} = \frac{\Delta{t}}{\gamma}<\Delta{t}.$$ This said, nothing whatsoever prohibits us from using the second figure in the introduction and the the second figure in the results. In such case we interpret the problem statement by refering to the second figure in the results, where we are given $\Delta{t'}$ and $\Delta{z'}$. From which, we have that $$\Delta{z} = \frac{\Delta{z'}}{\gamma}<\Delta{z'} \qquad \text{and}\qquad \Delta{t} = \frac{\Delta{t'}}{\gamma}<\Delta{t'}.$$ To re-iterate the elapsed time and elapsed distance of the two events from the frame of the muon is less than the corresponding time and distance in the frame of the earth.

In conclusion, given taht that one object is moving at a speed relative to another object, (1) it is true that the relative motion affect the changes in distance measured in each frame; and (2) irrespective of how one frames the matter, it is true that the construction of the Minkowski spacetime diagrams reveals the matter correctly.

Bibliography

1 N. Gray, A Student's Guide to Special Relativity, Cambridge University Press, 2022, p. 55.

Answer 9

Length contraction is indeed a symmetrical effect in SR, but the nature of the symmetry is such that one can easily misunderstand it.

The best starting point to understanding the effect is to consider that it arises from the relativity of simultaneity, as I will try to explain as follows.

Suppose you have a moving train. If you measure the position of the front of the train, and at the same time measure the position of the rear, then the distance between the two positions will correspond to the length of the train. However, if you measure the position of the rear of the train some time after you measure the position of the front, the difference between the two measurements will be less than the true length of the train, because the rear of the train will have moved forwards in the time between the two measurements.

That is how length contraction arises. If you have two positions 100km apart in one rest frame- let's call them X1 and X2- and you locate them at a fixed instant in some other frame through which they are moving, the fixed instant at X1 and X2 in the second frame actually corresponds to two different times at X1 and X2 in the rest frame. From the perspective of someone in the rest frame, you are locating point X2 after you have located point X1, so that you are not measuring the true distance between them.

In the case of the muon, if you consider the muon to be stationary and the Earth to be moving, a fixed distance of 100km in the Earth's frame might seem to be contracted to around 1km to the muon. In that case, a fixed distance of 100km in the muon's frame would appear to be 1km on Earth. So, if you had two muons travelling one behind the other, spaced 100km apart in their own frame, they would seem to be 1km apart on Earth.