Apparently physicists think that there is something inside black holes. Like a new universe or a link between dimension... But for me a black hole is no more than supermassive supercompacted matter. So my question is on which theoretical or observational bases these theory of what is inside a black hole lie on?
thanks!
(yes, I've seen Interstellar few days ago)
You are correct that physicists think a black hole is a link to another universe.
No, not really, that's just an attention grabbing headline. Physicists (most of them) don't believe black holes are links to other universes, apart from some fringe theories that I'll come back to. But let me explain where this misconception comes from. This absolutely fascinated me as a spotty youth - who wouldn't be fascinated by the idea that multiple universes might be real - so I'll spend a bit of time trying to explain this layman's terms. This will make the answer a bit long, but I think it's worth sticking with it.
The first, and key, thing to note is that real black holes are fearsomely complicated objects, so physicists tend to use simplified models of black holes. The simplest model, and the one we learn first, is the Schwarzschild metric. If you're describing things around a black hole the simplest way to approach this is consider distance from the centre, which we call $r$, and time, which we call $t$. If something is falling into a black hole we expect the distance $r$ to decrease with time and become zero at the moment you splat into the centre. So if we draw a graph to show something falling into the black hole it might look like:
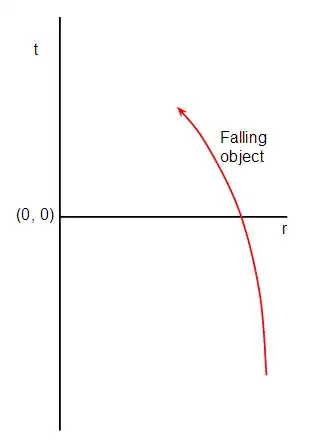
This shows time $t$ on the vertical scale, so increasing time moves up. The distance from the centre is on the horizontal scale.
Now we can define a zero of time whenever we want. For example the zero of our calendar is at midnight on the year zero AD. Times before this are shown as negative (or BC if it's a calendar). That's why I've put the zero of the time axis in the middle so time is positive in the top half and negative in the bottom half. However distance from the centre can only be positive because you can't get closer to the centre than zero. It doesn't make sense to have negative values of $r$, and that's why I've drawn the distance axis starting at zero.
So far so good, but it turns out that by choosing $r$ and $t$ as our coordinates we have oversimplified the physics of the black hole. In 1960 a couple of physicists called Martin Kruskal and George Szekeres discovered that to fully describe the black hole you need to use different coordinates called (unsurprisingly) Kruskal-Szekeres coordinates. These have a coordinate $u$ that is sort of like distance, and a coordinate $v$, that is sort of like time. But when you draw a graph like the one above you find that both $u$ and $v$ can be negative as well as positive, and a graph of an object falling into the black hole looks like:
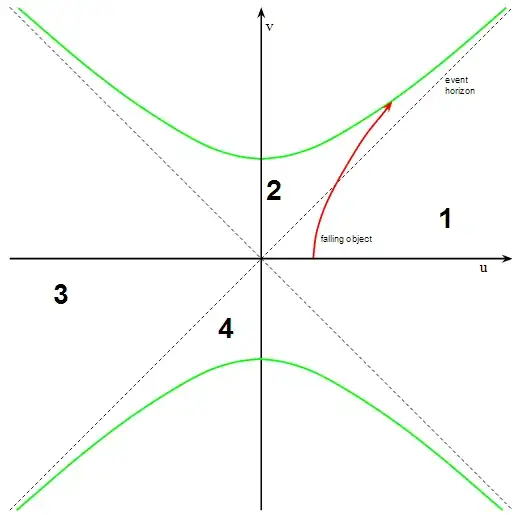
Explaining this diagram fully would take ages, so I'm going to cop out and just say that region ${\bf 1}$ is just the regular spacetime where we live, and region ${\bf 2}$ is inside the black hole event horizon. The curious thing is that our diagram now contains extra regions ${\bf 3}$ and ${\bf 4}$, and region ${\bf 3}$ is a region of ordinary spacetime just like ours, but which we can never get to.
So the Kruskal-Szekeres diagram shows two universes, regions ${\bf 1}$ and ${\bf 3}$, and they are joined by a type of wormhole called an Einstein-Rosen bridge. As it turns out nothing can cross the Einstein-Rosen bridge without travelling faster than light, and since that's impossible it means the two universes are forever isolated from each other. Still, the other universe is there.
In fact it gets even weirder than this. If we put an electrical charge on our black hole we get a Reissner-Nordström black hole, and this does allow you to travel to the other universes. I discussed this in my answer to the question Entering a black hole, jumping into another universe---with questions.
A rotating black hole does something similar, though the geometry is more complicated.
But I did say right at the outset that physicists don't really believe these other dimensions exist, which is sad and which was a great disappointment to me when I started learning general relativity - oh well.
The trouble is that the Schwarzschild metric I started with is a simplified model. For one thing it only applies if the black hole is unchanging i.e. it must have existed unchanged for an infinite time and must exist unchanged for an ininite time into the future. But we know no black hole can't be older than 13.7 billion years because that's how old the universe is. And we know black holes will eventually evaporate due to Hawking radiation, so they can't last an infinite time into the future.
And that spoils all the fun. It turns out a black hole of a finite age (probably) doesn't contain the extra regions of spacetime so there are no extra universes. The reason why you've heard about extra universes is because this subtlety tends to be lost on the popular press, science fiction writers and other groups with only a partial understanding of relativity. And of course because having extra universes is much more fun than not having extra universes!
I did say there were some fringe theories about black holes being gateways to other universes. This started in the late 60s with the work of a Russian physicist called M. A. Markov (I'm not sure what the M. A. stands for), who discovered that the spacetime describing a black hole could be seamless joined up to the spacetime describing an expanding universe. This is discussed to some extent in my answer to the question How does the friedmon solution to Einstein's equations resolve paradox of bounded infinities?. If you fell into a spacetime with this geometry you'd start by falling towards what looked like a black hole and certain death, but then you'd find you were drifting in an expanding universe just like ours.
But this is just a piece of clever geometry, and there was no physical model for why this particular geometry might actually exist. In the absence of any such model the obvious conclusion is that it doesn't. However some time later the American physicist Lee Smolin picked up the idea and proposed that it could happen due to quantum gravity effects, and that black holes really were gateways to new expanding universes. Smolin's theories are described in his book The Life of the Cosmos. Personally I don't believe a word of it, though I recommend the book as it's relatively easy reading and very entertaining.
There is no basis for such speculation. General relativity defines the event horizon of a black hole as the boundary from which nothing -- no matter, no light, no information -- can ever escape. Thus the question of what is inside a black hole becomes rather moot. The answer cannot even in principle affect us outside the event horizon.
Now black holes are fascinating objects, and some physicists debate endlessly about what happens when we throw quantum mechanics into the mix. But there are scarce few results from this line of thinking, other than some suggestions that maybe the universe only forms transient things that are very close to but not quite the ideal black holes we like to think about.
Certainly there is no observational evidence to speak of in this matter -- everything we could conceivably measure about real black holes with anything like our current technology is perfectly well explained without quantum effects.
As for new universes and other dimensions: These words get thrown around a lot in science fiction, but they don't mean much in science. If you go with the simple "everything that can be observed" definition of "universe," then by definition there can be no other universe to observe. So you'd have to come up with some other definition to even make sense of the idea of another universe. And "dimensions" just refers to how many space (3) and time (1) coordinates one needs to specify a location in the universe, rather than a "plane of existence" or whatever science fiction might use the term for.
