Since the early 2000s, Matthew Bate and collaborators have been producing smoothed particle hydrodynamic (SPH) simulations of collapsing clouds. The clouds have an initial uniform density, no net angular momentum, but a turbulent velocity field.
These clouds begin from rest and collapse under their own gravity to form hundreds of stars including many with spinning accretion discs and many binary systems of all shapes and sizes.
See for example http://www.astro.ex.ac.uk/people/mbate/Cluster/index.html
Turbulence begets vortices and vortices generally produce angular momentum.
So the question boils down to, if you hadn't imposed the turbulent velocity field to begin with, would a turbulent velocity field develop in a collapsing cloud? I believe the answer is yes; certainly numerical simulations would end up with turbulence if only because of numerical noise. Turbulence cannot be deterministically treated with Newtonian mechanics. To quote the Wikipedia page on turbulence, "Although it is possible to find some particular solutions of the Navier-Stokes equations governing fluid motion, all such solutions are unstable to finite perturbations at large Reynolds numbers. Sensitive dependence on the initial and boundary conditions makes fluid flow irregular both in time and in space so that a statistical description is needed." Where do these perturabations come from? Well if your cloud is asymmetric to begin with then there will clearly be interacting flows with different densities and velocities. Even if you started with an utterly uniform, symmetric cloud, quantum and statistical mechanics would ensure that the necessary perturbations were there.
Bate (2009) shows that the details of the imposed turbulence spectrum does not greatly influence the final outcome in terms of mass function and binary properties of stars and brown dwarfs produced in the simulation. Unfortunately, as far as I know, they have never simulated a cloud with no turbulence because such things do not exist in nature.
I fear this is a "how many angels can dance on the head of a pin" kind of question, because the required initial conditions will always be spoiled by quantum fluctuations at a minimum.
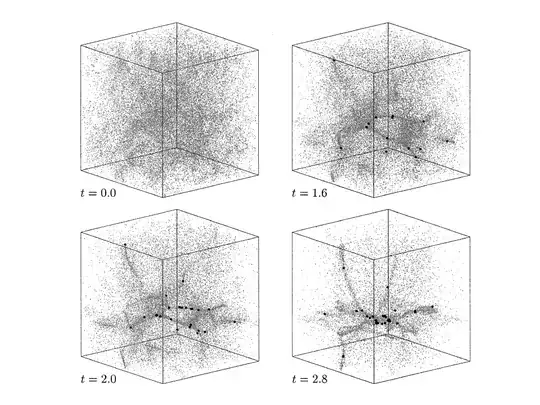
EDIT: I have managed to find a couple of fairly early SPH papers which deal with the collapse of a cloud that has a spectrum of Gaussian density perturbations but no imposed velocity fields. i.e. They start with asymmetric, inhomogeneous densities, but from rest. The simulation do not have a high enough resolution to follow things all the way down to binary systems and disks, but you can see from this sample picture below of the time evolution, that the gas is not collapsing along radially symmetric flow lines and therefore very complex structure arises which must have concentrations and "knots" of angular momentum, even though the initial cloud possessed none. It isn't really even turbulence that produces the complexity, just the gravitational collapse of an inhomogeneous structure.
Klessen et al. 1998, ApJ, 501, L205
Klessen & Burkert 2000, ApJS, 128, 287
That an asymmetric distribution of mass starting from rest will eventually produce subsytems with angular momentum has actually been known for a long time. I also found a paper by Szebehely & Peters 1967 called "Complete Solution of a General Problem for Three Bodies". In this, the initial setup is 3 masses at rest in a "Pythagorean triangle" - a right angles triangle with sizes 3,4,5 and masses in the ratio 3:4:5. The resulting evolution of this system leads to "In the final configuration two of the three participating bodies form a permanent binary, while the third body is ejected to infinity". i.e. a binary system with angular momentum is created from a system with zero initial angular momentum.
See also http://adsabs.harvard.edu/abs/1995MNRAS.273..751V ; http://adsabs.harvard.edu/abs/1991ARA%26A..29....9V
