9

I'm trying to understand the modern description of high-energy scattering processes involving hadrons in the initial states. The phenomenological parton distributions functions play a central role, and as I understand it at the moment, if we are e.g. talking about gluons, the function $G(x, Q^2)$ is the probability of finding a gluon with momentum fraction $x$ inside the hadron if the transmitted four-momentum is $Q^2$.

When these functions are plotted, I often encounter plots showing $x G(x, Q^2)$ instead of simply $G(x, Q^2)$. Why is this so? Is this just because the plots look a lot nicer if plotted this way? Or is there some deeper reason behind this that I haven't figured out yet?

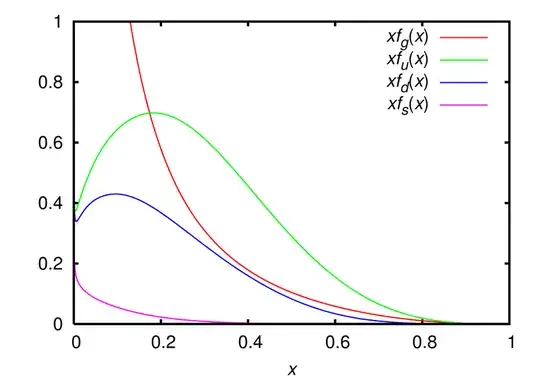
As an example, take a look at the plot used on Wikipedia. http://en.wikipedia.org/wiki/File:CTEQ6_parton_distribution_functions.png

(Picture from: http://en.wikipedia.org/wiki/File:CTEQ6_parton_distribution_functions.png)

AdamRedwine
  • 5,053
David M. R.
  • 555

1 Answers1

9

As you say, "$G(x,Q^2)$ is the probability of finding a gluon with momentum fraction $x$ inside the hadron if the transmitted four-momentum is $Q^2$." In other words, $G(x,Q^2)$ is a probability density function. As you can see from the article, in this case the expectation value of the variable is

$E[X] = \int_{0} ^{1} x\cdot G(x,Q^2) dx$

The plot of $x\cdot G(x,Q^2)$ then gives an intuitive sense of the "contribution" to the expectation value of the probability density function.

AdamRedwine
  • 5,053