Why does correlation length diverge at the percolation threshold?

Question

I'm reading a paper about electronic percolation. $p$ is the fraction of occupied bonds (or sites, depending on the model you're using, but I'll just use bonds), $p_c$ is the critical fraction of occupied bonds, and $G(x)\propto e^{-|x|/\xi}$ is the 2 point correlation function (the probability that if a site $x$ away from the origin is connected to it by some path of occupied bonds).

They state without any proof or explanation that $\xi$ is the correlation length and is equal to

$\xi\propto A^\pm_\xi |p-p_c|^{-\nu}$

and then later say that it has to diverge around $p_c$.

What's the physical reason for this, or a more intuitive picture? Why would it diverge from both directions ($p>p_c$ and vice versa)?

Answer 1

The correlation function $G(x)$ gives the average correlation between two lattice sites (one at the origin, the other at position $x$). That is, loosely speaking, it describes how much more likely it is for the site at position $x$ to belong to the same cluster as the origin than it would be for a site chosen randomly from across the whole lattice.¹

For subcritical bond percolation, all clusters are almost surely finite, and so the probability of two randomly chosen sites belonging to the same cluster is zero. The correlation function $G$ then simply describes how likely it is for two nearby sites to belong to the same cluster, as a function of their distance, and the correlation length parameter $\xi$ characterizing it can be thought of as the "typical size" of a cluster. The closer we get to the critical bond density, the bigger the clusters are, and so the bigger $\xi$ is.

For supercritical bond percolation, however, there will almost surely be a (single) infinite cluster, and so the probability of two completely randomly chosen sites belonging to the same cluster is non-zero. However, unless the bond density is 100%, the infinite cluster will not contain all sites, and so there will be some finite clusters as well.

As the probability of the origin belonging to one of these finite clusters is non-zero, sites close to the origin are still more likely to belong to the same cluster with it than sites far away, and this additional correlation between nearby sites is, again, given by the correlation function $G$ and its characteristic length scale $\xi$.

That is, for the supercritical case, we can interpret $\xi$ as the "typical size" of the finite clusters interspersed within the single infinite one. In this case, as the bond density increases from the critical value, the single infinite cluster will contain a higher fraction of all sites, and so the finite clusters within it get smaller, decreasing the correlation length.

^{1) There's some subtlety here, because of course we can't sample a site uniformly at random from an infinite lattice, but we can sample from, say, a normal distribution with variance $\sigma^2$, and take the limit as $\sigma^2\to\infty$; it turns out that, in this case, the limit indeed exists, at least for non-critical lattices.}

Answer 2

This is what the percolation threshold and phase transitions are all about, the emergence of diverging length scales with power laws - which makes the system scale invariant.

If you want physical intuition, play around with one of the many Ising model applets found on the web, like this one.

Answer 3

The particular value of the scaling exponent $\nu$, and the prefactor $A_\xi$ will depend on the lattice, and dimension you use to calculate, but the form $(p - p_c)^{-\nu}$ holds in a wide variety of geometries. For ease of calculation, I'll show how it works on the Bethe lattice, and how it's symmetrical about the critical point.

First, look at the Bethe lattice

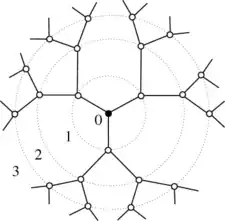
Notice that is has no loops, so there is a unique path from any site $i$ to any other site $j$.

The probability that any two sites $i$ and $j$ are connected is equal to the probability that each is occupied ($p\times p = p^2$), times the probability that every site on the path connecting them is occupied, which is $p^{d(i,j)}$, where $d(i,j)$ is the number of sites between sites $i$ and $j$.

Let's say that site $i$ is the origin, and $j$ is some point $r$ sites away, then there are $r-1$ sites between them, and the probability they're connected is $c(r) = p^2\times p^{r-1} = p^{r+1}$. We need to multiply this by the number of points that are $r$ sites away from the origin which, for the lattice in the figure, is $3\times 2^{r-1}$.

Thus, we have the correlation function given by $$g(r) = 3\times2^{r-1}p^{r+1}$$

We can rewrite this as $$g(r) = \frac{3}{2^2}\left(2p\right)^{r+1} \sim e^{\left(r+1\right)\ln 2p}$$

Clearly, the correlation shrinks to zero when $2p < 1$, and becomes infinite when $2p > 1$, so we have $p_c = 1/2$.

Now, we can say $$g(r) \sim e^{r\ln p/p_c}$$ which resembles the form in your question, we just need to introduce a minus sign to make the correspondence complete.

The correlation length is defined to be the distance at which the probability of a site being connected to the origin falls to a level $1/e$, this is quite clearly given by $$\xi = -\frac{1}{\ln (p/p_c)} = \frac{1}{\ln (p_c/p)}$$ which for $p$ close to $p_c$ can be expanded using the Taylor series for $\ln(1+x)$, a la

$$\ln p/p_c = \ln \left[ \left(p_c - p\right)/p + 1\right]\approx \frac{p_c - p}{p}$$ Thus, we finally have $$\xi \approx \frac{p}{p_c - p} \propto \left(p_c - p\right)^{-1}$$

Note that each site in the Bethe lattice used here branch out to 3 other sites. If instead, each site branched to $z$ sites, we'd just replace every 3 and 2 in the above argument with $z$, and $z-1$, and our result would be general (and you'd find $p_c = \left(z-1\right)^{-1}$).

Now, the correlation length obviously goes to infinity for $p > p_c$, however, if you focused on the correlation length of sites that are in finite clusters (i.e. ignore the infinite clusters), then you'd get the same form for the correlation length. As you go above the critical point, the probability of being in a large, finite cluster gets smaller and smaller, and it is only likely to be in an infinite cluster, or in a very small finite cluster. Obviously, the average finite cluster size decreases until $p=1$ when it becomes zero (everything is in the infinite cluster). This is not a quantitative argument, but demonstrates the bi-directionality of the correlation length scaling.