Light can crisscross in all directions.
Source: Can photons pass through each other?
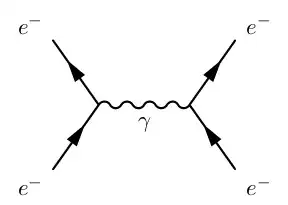
In a given volume, we can have light throughout, such that there is no space with no light in it (with the electron which is to be seen).
Light gets scattered or reflected from the electron, in either I hope we can expect absorption and re-emission of photon (and thus use this to see the electron with appropriate technology).
Source (covers only an idea of quantum picture of reflection) : http://arxiv.org/abs/1207.0998
(I couldn't find better source on this, any related source or suggestion of reading w.r.t this, particularly on the difference between quantum picture of reflection and scattering, will be of interest to me)
Absorption and re-emission involves time delay (around $10^{-23}$ to $10^{-20}$ s).
Source: http://arxiv.org/abs/1207.0278
This time delay won't affect if the photons are incident continually. With this thought experiment, can we track the electrons definite path?