2

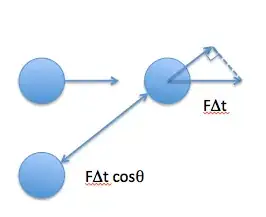
Let us consider a system of 2 identical spherical bodies connected by a massless string that is taut. If one body is placed at the origin then the other is placed at some coordinate $(x,y)$. The string that connects these bodies makes an angle $Z$ with the $x$ axis. Now consider another identical sphere that moves with some velocity $V$ parallel to $x$ axis such that it will eventually collide with the body placed at $(x,y)$. The collision is elastic.

Clearly in this case the string exerts some impulse that has an horizontal component. My questions are as follows:

  1. does impulse act on both the bodies connected by the string? Is it the same amount?
  2. Momentum cannot be conserved for the two colliding spheres as there is horizontal impulse?
  3. What is the goal of impulse? (like friction opposes motion of the body in contact always what does this impulse do?)
Mostafa
  • 4,034
Sashurocks
  • 162

1 Answers1

3

If the string is massless and taut, then the wave velocity is infinite - that is, a component of the force at one mass will immediately be felt at the other mass. But to answer your first question, not all the force of the impact will be transmitted along the string, as made clear by this diagram:

enter image description here

As for your second question: momentum for the system is always conserved. In this case you need to look at the horizontal components of momentum (shared between the two masses) and the vertical component (one will start to move up, the other starts to move down).

As for the third question - after this collision, the system of two masses will be moving to the right (center of mass picks up net momentum to the right) and it will be rotating clockwise (because of the action of the tension that results in the ball that was hit experiencing a downward component of force, and the other ball experiencing an upward force).

Community
  • 1
Floris
  • 119,981