Why are non-relativistic methods used in binary pulsar systems (gravitational waves)?

Question

Although gravitational waves are a subject of the General Relativity, why do most books use Newtonian equations of motion for power radiated and rate of change of eccentricity calculations? In most books ("Gravitation, Foundation and Frontiers", by T Padhmanabhan for instance) they calculate the energy-momentum tensor for fields through a General Relativistic approach. However, they switch to a non-relativistic approach once they come to the binary pulsar. If everything can be done through non-relativistic Newtonian (or Keplerian) methods, then why do we need to calculate everything in General Relativity?

Answer 1

Systems of moving masses should emit gravitational waves in analogy with the emission of electromagnetic waves by a system of moving charges. Early attempts to calculate the energy in these waves were based on the use of pseudostress-energy tensor for finding the energy flux.

Example:

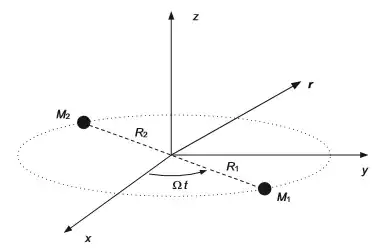
If we assume that the two bodies making up the binary lie in the x-y plane and their orbits to be circular, the non-vanishing components of the quadrupole tensor are:$$\boxed{Q_{xx}=-Q_{yy}=\frac{1}{2}(\mu)a^{2}\cos2\Omega t}$$ and $$\boxed{Q_{xy}=Q_{yx}=\frac{1}{2}(\mu)a^{2}\sin2\Omega t}$$ Where $\Omega$ is the orbital velocity, $\mu=\dfrac{m_{1}m_{2}}{m}$ is the reduced mass and where $m=m_{1}+m_{2}$ Gravitational waves carry energy and cause a deformation of space-time. The stress-energy carried by these waves cannot be localized within a wavelength; rather it can be said that a certain amount of stress-energy is contained in a region of space which extends over several wavelengths.

The disadvantage associated with this method is that always a coordinate system can be chosen such that the energy flux would vanish in it; also this method is only valid for systems which are not gravitationally bound. So, the case of binaries remained unsolved back then.

Sir Arthur Eddington found radiation form systems by calculating the radiation reaction of the system itself. This too was not valid for gravitationally bound systems. For situations in which radiation is constant, the above mentioned methods agree. However, for cases where the radiation is time-dependent, different methods are to be used. Analogy in the results obtained occur in electromagnetic radiation theory.

One approach to solve gravitational radiation is to consider only the exact solutions of the nonlinear field equations of GR. These equations are expanded in powers of gravitational coupling constant because of the weakness of the gravitational interaction. Once the field equations of GR are expanded in terms of the gravitational coupling constant, the integral conservation laws of energy, momentum, and angular momentum can be calculated. For a non-relativistic system, the radiation is given in terms of time derivatives of the matter distribution of the system. The binaries are treated as a system of two point masses moving in elliptical orbits under their mutual gravitational attraction. The system of binaries decay as a result of gravitational radiation and the changes in the orbit can be found during such a decay. Given the field equations are valid:

$$\boxed{R_{\mu \nu}-\frac{g_{\mu \nu}R}{2}=-8\pi GT_{\mu \nu}}\tag{1}$$ Let $g_{\mu \nu}=\delta_{\mu \nu}+h_{\mu \nu}$, the field equations can be expanded in powers of $h_{\mu \nu}$ to get: $$\boxed{\bar{h_{\mu \nu,\lambda \lambda}}-\bar{h_{\mu \lambda, \lambda \nu}}-\bar{h_{\nu \lambda \lambda \mu}}+\delta_{\mu \nu}\bar{h_{\lambda \sigma,\lambda \sigma}}=-16\pi GS_{\mu \nu}}\tag{2}$$ $S_{\mu \nu} $ is uniquely define de and the divergence of the LHS of the equation vanishes. Hence $S_{\mu \nu, \nu}=0$ and conservation laws can be written.

The invariance of $(1)$ under arbitrary coordinate transformations implies that one may always choose a coordinate system in which $\bar{h_{\mu \nu, \nu}}=0$. This would simplify the case but then equation $(2)$ would become an inhomogeneous wave equation!

We can assume that the field equations are valid for large distances from the system, and the gravitational potentials $h_{\mu \nu}$ are inversely proportional to the distance From the system for large distances, then the energy of the system must decrease a small a result for the radiation of the gravitational waves, regardless of the coordinate system or conditions used.

Hence, in non-relativistic approximation, the radiation is the same as that found in gauge $\bar{h_{\mu \nu, \nu}}$.

Edit:

Just realised that this question is 2 years old,for anyone interested please check this out, this paper

Answer 2

Gravitational Waves are predicted by GR. There are no gravitational waves in Newton's theory.

A wild guess is that the author of this book uses classical potential theory to explain multipole expansion of GW's (as known from electrical potentials, basically fourier series on a sphere) and in the GW case for the hypothetical graviton spin 2, you should get a quadrupole moment.

Answer 3

If everything can be done through non-relativistic Newtonian (or Keplerian) methods, then why do we need to calculate everything in General Relativity?

The success of General Relativity shows that it is relevant and has to be taken into account in gravitational problems. But at the same time, the GR gravitational equations reduce to Newtonian equations where the gravitational fields are weak enough, and velocities non relativistic for the particular problem at hand.

In the Hulse-Tailor binary for example:

Orbital velocity of stars at periastron (relative to center of mass): 450 km/s

To use the mathematical panoply of general relativity when, for the accuracies needed for the problem, the newtonian approximation is good enough is a waste of intellectual effort.

So the guess is, since there is no link to read the specific problem, that the newtonian approximation is good enough for the problem at hand. It all depends on the accuracies needed. General Relativity is taken into account in the GPS system, just because great accuracy is needed, though I have not seen it used on the tide tables.