My prof asked me to do a graphic of a given function and I have to just to vary the gravitational acceleration $g$ and the height $H$. If I know the interval in which $H$ is defined :$[500,2000]m$, how can I find the value of $g$? Sorry for my English!
Asked
Active
Viewed 1,509 times
2 Answers
3
Small elaboration on t.c's answer:
If you say that
$$F = \frac{G\ M_e}{R_e^2}m = g\ m$$
at the surface of the earth $R_e$, then at other heights you can write (for $h << R_e$):
$$\begin{align} \\ F &= \frac{G\ M_e}{(R_e+h)^2}m\\ &= \frac{G\ M_e}{R_e^2(1+\frac{h}{R_e})^2}m\\ &\approx\frac{G\ M_e}{R_e^2}(1-2\frac{h}{R_e})m\tag1\\ &= g (1 - 2\frac{h}{R_e})\tag2\\ \end{align}$$
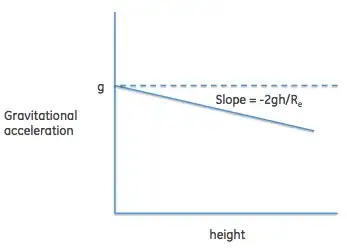
The trick at (1) is to use a first order expansion (the first term of the Taylor expansion) to show the relationship between the force of gravity at sea level and at greater heights. So you see it drops off linearly with height, and the coefficient of the slope is twice the ratio of the height to the radius of the earth. Now you don't need tons of significant figures to calculate the drop with height - because you can take the $g$ term out altogether and draw the sketch:
Floris
- 119,981
2
You can use the Newton's law of gravitation which is given by:
$$F = G \frac{m_1 m_2}{r^2}=\left(G \frac{m_1}{r^2}\right) m_2$$
The gravitational constant, $G$, the weight of Earth, $m_1$, and the radius are constants, so:
$$G \frac {m_1}{r^2}=(6.6742 \times 10^{-11}) \frac{5.9736 \times 10^{24}}{(6.37101 \times 10^6)^2}=9.822 = g$$
You can adjust $r^2$ according to the height you require. The higher the $H$, the higher the $r$, and the lower the $g$.
t.c
- 1,552