I won't try to defend Feynman's derivation, which seems strangely non-relativistic. (A similar argument is used by Schwartz in his "Principles of Electro-Dynamics".)
However, I will defend the result (the Liénard-Wiechert potentials), and specifically claim that they are not in conflict with your discrete charge example, at least for the case of uniform motion.
The argument proceeds in two steps: 1) calculation of the potentials via relativity, 2) comparison with the Liénard-Wiechert potentials.
1) For a discrete charge in uniform motion, the key is that $(\phi, \mathbf {A})$ form a relativistic 4-vector potential, which transforms like any other 4-vector under a Lorentz transformation. In particular, $\phi$ transforms like the time $t$.
Consider, in the "primed" coordinates, a stationary discrete charge at the origin. Its potential $\phi'$ is simply:
$$ \phi'(x',y',z',t') = \frac{q}{4 \pi \epsilon_0 r'}
= \frac{q}{4 \pi \epsilon_0} \frac{1}{\sqrt{x'^2 + y'^2 + z'^2}} \, , \,\, \mathbf {A'}=0 $$
Now define the "unprimed" coordinates as boosting the charge into motion with speed $v$ and velocity $\mathbf{v}$ parallel to the $x$-axis, so that the coordinate Lorentz transformation reads:
$$ t'= \gamma \left( t - \frac{v}{c^2}x \right) \, , \, x' = \gamma (x - vt ) \, , \, y' = y \, , \, z' = z \, , \, \gamma=\frac{1}{\sqrt{1-(v/c)^2}}$$
Then, applying this same Lorentz transformation to the 4-potential, we get:
$$ \phi(x,y,z,t) = \gamma \phi' (x', y', z', t') = \gamma \frac{q}{4 \pi \epsilon_0}
\frac{1}{\sqrt{\gamma^2(x-vt)^2 + y^2 + z^2}} \, , \,
\mathbf{A} = \gamma \frac{\mathbf{v}}{c^2} \phi'= \frac{\mathbf{v}}{c^2} \phi$$
as the 4-potential of a charge with constant velocity $v$ in the $x$-direction. Actually, Feynman performs this same calculation in Section 25-5.
2) The kicker is that this expression is precisely what one gets from the Liénard-Wiechert potentials, as Feynman demonstrates in Section 21-6.
As I said, I'm not going to try to defend Feynman's derivation. I suspect a relativistic alternative could be developed that gives the same, correct, Liénard-Wiechert potentials as a result (but I don't have one in hand).
Update: Ah, Jackson (sections 12.11 and 14.1) develops a general expression for the potentials in the Lorenz gauge that is directly applicable to your point charge example. In Feynman's notation:
$$A^\mu(1,t_1) = \frac{1}{4 \pi \epsilon_0 c^2}
\int {\mathrm dt_2~\mathrm dV_2 \frac{\delta(t-t_2-r_{12}/c)}{r_{12}} J^\mu(2,t_2)} $$
where the four-vectors $A^\mu = (\phi/c, \mathbf{A})$ and
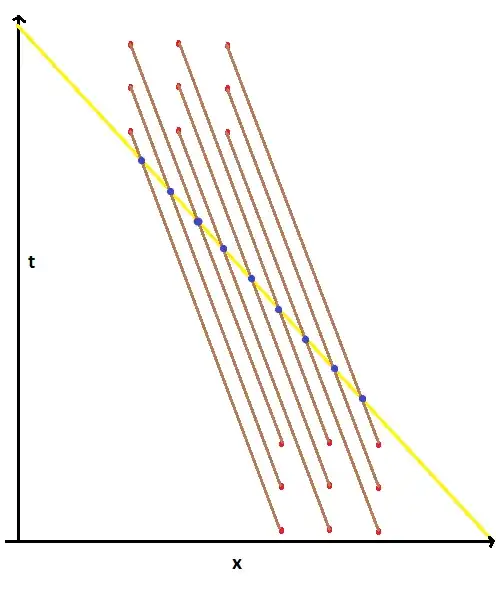
$J^\mu=(\rho c, \mathbf{J})$. The $\delta$-function picks out exactly the retarded points on the past light cone of the observation point. [It will also turn out to introduce the non-obvious "stretching factor" that arises in Feynman's development.]
For a point charge,
$ \rho(\mathbf{x},t)=q \, \delta[\mathbf{x}-\mathbf{r}(t)] $,
the four-current is:
$$ J^\mu(x) = qc \int { \mathrm d \tau \,U^\alpha (\tau) \delta^{(4)}[x-r(\tau)] } $$
where $ \tau $ is the particle's proper time,
$x^\mu=(ct,\mathbf{x})$, $r^\mu(\tau) = (c\tau, \mathbf{r}(\tau))$,
the four-velocity $U^\mu = ( \gamma c , \gamma \mathbf{v} )$, and
$ \gamma = 1/\sqrt{1-(v/c)^2} $. (The "extra" $c$ at the front of $J^\mu$ is needed to balance the $ct$ within the $\delta$-function; these two $c$'s cancel when the integration over $t$ is performed.)
Specializing to the potential $\phi$ and integrating over the 4-volume, we get:
$$ \phi(1,t) = \frac{q}{4 \pi \epsilon_0 c}
\int { \mathrm d \tau \, U^0(\tau) \frac{\delta(t - t'(\tau) - r_{12}(\tau)/c)}{r_{12}(\tau)} } $$
where $t'$ is the retarded time.
Now to evaluate that delta function, we use the rule:
$$\delta(f(\tau)) = \sum_i \frac{\delta(\tau-\tau_i)}
{\left| \left( \frac{\mathrm df}{\mathrm d\tau} \right)_{\tau=\tau_i} \right|} $$
where $\tau_i$ are the zeros of $f(\tau)$. Here there is only one zero (that is, one contributing point from the past light cone), and
$$ \frac{df}{d\tau} = \frac{\mathrm d}{\mathrm d\tau}{\left( t - t'(\tau) - r_{12}(\tau)/c) \right)}
= - \gamma (\tau) + \gamma (\tau) v_r (\tau) /c
= - \gamma (\tau) ( 1 - v_r (\tau) /c ) $$
where $v_r$ is the component of the charge's velocity towards the observer (same definition as Feynman's). Note the appearance of the "stretching" or "over-counting" factor.
Well, the $\gamma$ in $U^0$ in the numerator cancels the $\gamma$ arising in the denominator from the $\delta$-function, and we are left with
$$ \phi(1,t) = \frac{1}{4 \pi \epsilon_0} \frac{q}{r_{12}'} \frac{1}{1 - v_r'/c }$$
where the prime denotes evaluation at the retarded time.
So, there's no contradiction: a correct relativistic treatment of a point charge gives the same result as Feynman's analysis. The "over-counting" that concerned you in Feynman's development is just an approximation to the exact behavior of the light-cone delta-function, reducing to it in the limit. (I think it's akin to calculating a function's derivative by changing the argument by a small $\delta$, calculating the rise/run ratio, and then letting $\delta$ go to 0.)