I'm struggling to understand the paper PRL 106:136806 (2011). It is highly cited, but I cannot reproduce their results. Let me quickly summarize the authors' argument and raise my questions.
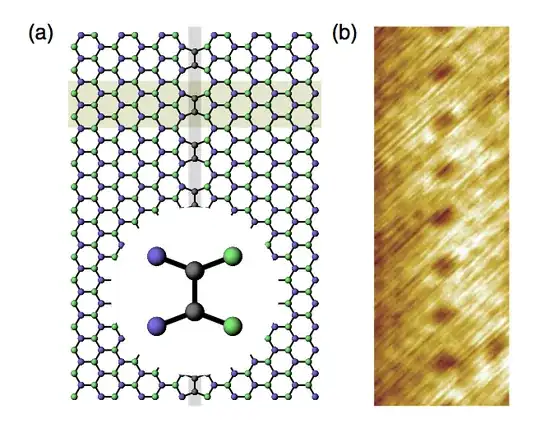
It is all about the transmission of an electron through the line defect connecting two graphene half planes shown in the above figure. The authors claim that, the transmission depends on the valley index $\tau = \pm 1$. Their reasoning goes like this. They pick up an electron (with positive energy) in valley $\tau$ and wrote the state vector as $$|\Phi_{\tau}\rangle = \frac{1}{\sqrt{2}}(|A\rangle + ie^{-i\tau\alpha}|B\rangle).$$ Here $\alpha$ is the angle of the wave vector $\vec{q}$ relative to the corresponding Dirac point. To make sense, I have to interpret $$\langle\vec{r}|\nu\rangle = e^{i(\vec{K}_{\tau}+\vec{q})\cdot\vec{r}_{\nu}}, \ \nu =A,B.$$ Here $\vec{K}_{\tau} = (0,\tau \frac{2\pi}{3})$. They rewrite $$|\Phi_{\tau}\rangle = \frac{1+ie^{-i\tau\alpha}}{2}|+\rangle + \frac{1-ie^{-i\tau\alpha}}{2}|-\rangle,$$ with $$|\pm\rangle = \frac{1}{\sqrt{2}}(|A\rangle \pm |B\rangle).$$ Now they assert that, $$\langle\vec{r}|-\rangle \equiv 0$$ for $\vec{r}$ on the line defect. Thus, only $|+\rangle$ contributes to transmission. So, they conclude $$T_{\tau} = |\langle +|\Phi_{\tau}\rangle|^2 = \frac{1}{2}(1+\tau\sin\alpha).$$ Here I have a question, why does $\langle\vec{r}|-\rangle$ vanish on the line defect? This is absolutely incomprehensible to me.
Near the end of this paper, the authors gave a calculation, which I do not understand either. They treat the line defect as a channel and the half-graphene planes as electrodes. Then they wrote $$T_{\tau} = \langle\tau|\Gamma G \Gamma G^{\dagger}|\tau\rangle.$$ Here $|\tau\rangle$ is the state vector for the blue atoms shown in the figure, $G$ the retarded Green's function for the channel (line defect) and $\Gamma = i(\Sigma - \Sigma^{\dagger})$ the broadening matrix in terms of the self-energy $\Sigma$. Although I have lots of experience with Nonequilibrium Green's functions for transport calculations, I do not understand this expression. According to my understanding, the operator $\Gamma G \Gamma G^{\dagger}$ acts on the state vectors of the channel, not on the electrodes. But the authors act it on $|\tau\rangle$, which is a state vector of the electrodes.
Could you help me? Many thanks in advance !