Is mass in particle physics classical or relativistic?

Question

Is the concept of mass in particle physics relativistic (i.e. mass as described by general relativity) or classical (i.e. mass as described by classical Newtonian physics)?

Answer 1

For the most part, particle physics adhere to the convention of very small lengths. In such lengths, every manifold that is used in general relativity, conforms to Minkowski space-time metric.

As a result it is customary to disregard the overall curvature implied by general relativity and use covariant derivatives that neglect the Christoffel connections.

However, in particle physics, as opposed to Newtonian, the mass term is coupled to the square of the coordinate, as opposed to being a part of the kinetic term.

$$ \mathcal{L}=\frac{1}{2}\left(\partial_\mu\phi\right)^2 + m^2\phi^2 $$

So as to derive the Klein-Gordon equation: $$ P_{\mu}P^{\mu}=m^2 $$

So the answer is: neither.

Answer 2

There are two kinds of mass :

1) the rest mass

i.e. the invariant mass of a system described by a relativistic four vector

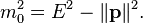
The invariant mass of elementary particles, which are the foundation stones of the standard model characterizes them uniquely. Composite particles as the proton for example have an invariant mass that comes from the addition of the individual four vectors of the component quarks and gluons.

2) The relativistic mass

the famous E=mc^2

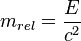
This is not very useful for particle physics and has fallen out of use.

In conclusion, the mass used for particle physics is the invariant mass of special relativity, the "length" of the relativistic four momentum vector .