So we have one of Friedmann's equation:
$$\rho_c = \frac{3H^2}{8\pi G}$$
Using This website, resources where gathered for specific times in the universe. The resources being the Hubble constant at the specific times (i.e. 3.38By). The critical density was worked out for the specific times using the Hubble constant. The critical density was in Kg/m-3 units and was converted into amu/m-3 units, by timing the value by 6.02214129 × 10^26. I then graphed the values:
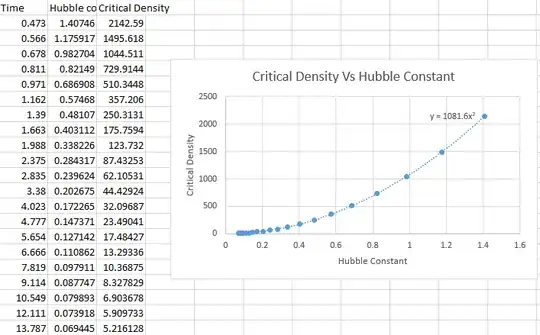
I could then conclude from this data that (equation of the line): $$\rho_c = E H^2$$ $$H^2= \frac{\rho_c }{E}$$ Where E = 1081.6, isn't this a much simpler equation to work out the critical density or Hubble constant? Not saying one is better than the other, but just an idea. For further investigation i will use the equation to find the Hubble constant at 13.79By where the critical density is 5.2 amu/m-3: $$H^2= \frac{\rho_c }{E}$$ $$H^2= \frac{5.216128}{1081.6}$$ $$H= \sqrt{0.00482}$$ $$H= 0.069445$$ And we convert this from s-1 mpc to km/s mpc, through google, or times by 977.6 (google is better though). The final awnser we get is: H = 67.9km/s mpc. And if we refer to the Planck Mission where they observed the Hubble constant to be within 67.13 and 68.57km/s mpc, which corresponds to the answer we have through the new equation. Does this 'new' equation have any relevance in physics at all?