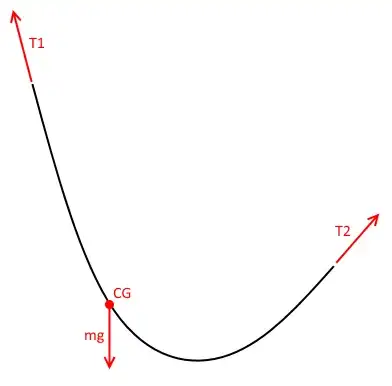
Since the cable is not moving horizontally you know the horizontal component of tension is the same at both ends. The total tension is the horizontal component divided by the cosine of the angle. So the ratio between the tensions is the ratio of the cosines. Since you know the shape of the curve you should be able to take it from here.
UPDATE
The general equation for a catenary (with lowest point at x=0) is
$$y = a \cosh \frac{x}{a}$$
Where
$$a = \frac{H}{w}\\
H = \text{horizontal tension}\\
w = \text{weight per unit length}$$
For a given horizontal distance and vertical displacement, we have to figure out the location of the lowest point and the tension - two equations, two unknowns.
From wikipedia.org/wiki/Catenary#Determining_parameters:
Given $s$, $v$, and $h$, then $a$ can be solved for numerically:
$$\sqrt{s^2 - v^2} = 2a \sinh \frac{h}{2a}, a > 0$$
where
$h$ is the horizontal distance between ends,
$v$ is the vertical distance between ends,
$s$ is the length of the cable, and
$a$ is the y coordinate of the lowest point.
Next, we just need to find the position of the lowest point relative to the ends. To get the actual locations of $x_1$ and $x_2$ (the horizontal distances from the lowest point to the the left and right ends, respectively) you now have to solve
$$\begin{align}\\
v &= a (\cosh \frac{x_2}{a} - \cosh \frac{x_1}{a})\\
h &= x_2 + x_1 \tag1 \\
v &= a\left(\cosh \frac{x_2}{a} - \cosh \frac{x_2-h}{a}\right) \tag2
\end{align}$$
Solve (2) for $x_2$ then substitute into (1) to get $x_1$
Finally, the ratio of tensions comes from the ratio of cosines of the angle at the point of suspension:
$$\frac{T_2}{T_1} = \frac{\cos\theta_1}{\cos\theta_2}$$
We know the tangent at $x$ is given by
$$tan\,\theta = \frac{dy}{dx} = \sinh \frac{x}{a}$$
Combine with the trig identity
$$cos\,\theta = \frac{1}{\sqrt{1+\tan^2\theta}}$$
You finally obtain
$$\frac{T_1}{T_2} = \sqrt{\frac{1+\sinh^2\frac{x_2}{a}}{1+\sinh^2\frac{x_1}{a}}}$$