Obviously this is impossible in relativity; however, if we ignore relativity and use only Newtonian mechanics, is this possible? How (or why not)?
4 Answers
The answer is yes in some unintersting senses: Take two gravitational attracting point particles and set them at rest. They will attract each other and their velocity will go to $\infty$ in finite time. Note this doesn't contradict conservation of energy since the gravitational potential energy is proportional to $-1/r$. This isn't so interesting since it's just telling you that things under gravity collide. But its technically important in dealing with the problem of gravitationally attracting bodies.
Now a more intersting question: Is there a situation where the speed of a particle goes to infinity without it just being a collision of two bodies?
Suprisingly, the answer to this question is yes, even in a very natural setting. The great example is given Xia in 1995 (Z. Xia, “The Existence of Noncollision Singularities in Newtonian Systems,” Annals Math. 135, 411-468, 1992). His example is five bodies gravitational interacting. With the right initial conditions one of the bodies can be made to oscillate faster with the frequency and amplitude going to infinity in finite amount of time.
Added
Here is an image. The four masses $M$ are paired into two binary systems which rotate in opposite directions. The little mass $m$ oscillates up and down faster. It's behavior becomes singular in finite time.
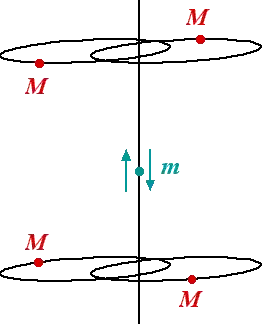
- 7,017
If by "ignoring relativity", you mean ignoring the fact that nothing can move faster than the speed of light, then the answer is still no.
Since kinetic energy is proportional to the square of the speed, infinite speed would mean infinite energy, which you cannot provide, whatever the amount of time you are considering.
- 259
Lab Reference Frame
Let's start assuming a force is exerted on the object from equipment "lab" reference frame, meaning that there is negligible recoil on the lab frame from accelerating the object. Not only is it the case that $F=ma$, but the power delivered to the object grows as $P=v F$. Take a device like the large hadron collider, and just completely wave off the technical difficulty of applying force to an object of progressively increasing velocity, and let's not the following.
$$v' = a = \frac{F}{m} = \frac{P}{v m}$$
The requirement is that $v \rightarrow \infty$ in a finite time. You know, just for fun let's use an actual functional form.
$$v(t) = -\frac{1}{t}$$
For t from $-\infty$ to $t=0$.
$$P = m v' v = -\frac{m}{t^3}$$
So the power delivered must increase at the hilariously fast rate of $1/t^3$ as $t$ goes to zero, not that it matters because we all knew this would result in requiring infinite energy, but this just shows exactly how intangible it is.
Rocket
In the case of a rocket the propellant has to be hauled along with the payload, but the tradeoff is that you then don't have the $P=v F$ proportionality, since the propellant itself is still moving after being ejected. The equation of motion for a rocket that starts with mass $M$ and ends with mass $m$, ejects propellant with speed $v_e$ is as follows. I'll add in the approximation for $M \gg m$, because obviously that must be the case since we're talking about going to infinity.
$$v = v_e \ln{ \frac{M}{m} } $$
This is certainly interesting. It is interesting to note that the speed the rocket can reach is proportional to the speed the propellant is ejected at, which is also not limited by the speed of light. The energy required to expel that propellant also isn't a problem (haha) because it is not the case that $E=mc^2$ in this world. But it would be skirting the problem to say that the propellant is ejected at infinite speed, so we still seek a way for the above expression to limit to infinity with $v_e \neq \infty$. But we would also really like $\frac{M}{m} \neq \infty$, because that would require either an infinitely large starting mass or an infinitely small ending mass. Neither of these options are appealing, unless atoms also don't exist in this world, allowing us to use fractal math to claim that an infinitely small chuck of something went to infinite speed.
To the extent that we don't make these absurd assumptions, your request is impossible, even given the already absurd assumption of allowable superluminal speed.
- 21,318
It sounds like the answer is yes for particles with mass but zero physical extent. I assume if the particles have finite extent (or we bring in quantum mechanics), then the answer is no, as it would be if we brought in relativity.
- 1