Visualisation of formation of electromagnetic waves

Question

1. Recently I am studying electromagnetic waves, and I am wondering why it is formed by acceleration of electric charges?

2. Can the EM waves be formed by other movements of electric charges, such as at a constant velocity?

3. And also, is there a way to visualize the formation of EM waves?

Answer 1

Question: Why do accelerating charges radiate, and can moving charges with zero acceleration also produce electromagnetic radiation?

Quick Answer: Only accelerating charges (and changing currents) produce electromagnetic radiation. The power of fields generated by charges with zero acceleration dies out at far distances.

Full Answer: The full answer to this question involves deriving the electric and magnetic fields for a point charge with nonzero velocity and acceleration. It can be shown that the electromagnetic power far away from the source charge is only nonzero if the charge is accelerating.

Electrostatics

In physics we can always find the rest frame of the particle (i.e., the frame in which the particle appears stationary ($\textbf{v} = \textbf{0}$ and $\textbf{a} = \textbf{0}$). In this frame where the particle is located at $\textbf{r}'$, we can calculate the electric and magnetic fields with the mathematical machinery of electrostatics. Assuming no external sources, the electric field (also known as the Coulomb field) is given by

$$ \textbf{E}(\textbf{r}, t) = \frac{q}{4 \pi \epsilon_0}\frac{\textbf{r} - \textbf{r}'}{|\textbf{r} - \textbf{r}'|^3}, $$

and the magnetic field is

$$ \textbf{B}(\textbf{r}, t) = 0. $$

Electrodynamics

However, for an arbitrary frame of reference, neither the velocity $\textbf{v}$ nor the acceleration $\textbf{a}$ are required to be $\textbf{0}$. In these frames, the easiest way to calculate the fields is by first finding the retarded potentials. Without going into too much detail, these are electric ($\phi$) and magnetic ($\textbf{A}$) potentials, in the Lorentz gauge condition, generated by the particle at the retarded time

$$ t_r = t - \frac{1}{c}|\textbf{r} - \textbf{r}'|. $$

The retarded time is used due to the fact that it takes a finite amount of time for the $\textbf{E}$ and $\textbf{B}$ fields to respond to the charge's motion (thanks to the finite speed of light, $c$). For convenience, we will introduce similar notation to Griffiths$^1$. Let $\textbf{R} \equiv \textbf{r} - \textbf{r}'$ and let $\textbf{U} \equiv c \frac{\textbf{R}}{R} - \textbf{v}$. The resultant fields are:

$$ \textbf{E}(\textbf{r}, t) = \frac{q}{4 \pi \epsilon_0} \frac{R}{(\textbf{R} \cdot \textbf{U})^3} [(c^2 - v^2)\textbf{U} + \textbf{R} \times (\textbf{U} \times \textbf{a})], $$

$$ \textbf{B}(\textbf{r}, t) = \frac{1}{c}\frac{\textbf{R}}{R} \times \textbf{E}. $$

Electromagnetic Radiation

Electromagnetic radiation, as defined in Griffiths$^1$, is the energy transfer (power) of the fields far from the source(s). Informally, it is the electromagnetic power that "survives at infinity." Mathematically, we can define the radiated power as

$$ P_{radiation} = lim_{r \to \infty} P(r), $$

where $P(r)$ is the flux of the the Poynting vector $\textbf{S}$ through a sphere of radius $r$. We will consider the following argument for why only accelerating charges produce radiation. Holding $\textbf{S}$ constant, we see that the flux increases as $r^2$ (due to the surface area of the sphere). For $P \neq 0$, we require that $S$ falls off as $1/r^2$ or less. For a point charge, $S \propto E^2$, so we are left with the requirement that the electric field decays no faster than $1/r$. Scanning the equation for the generalized electric field, we see that only the second term

$$ \textbf{E}_{r} = \frac{q}{4 \pi \epsilon_0} \frac{R}{(\textbf{R} \cdot \textbf{U})^3} [\textbf{R} \times (\textbf{U} \times \textbf{a})], $$

decreases slowly enough (the other term falls off as $1/r^2$). This is due to the presence of $\textbf{R}$ ($\equiv \textbf{r} - \textbf{r}'$) in the cross product. This term is known as the radiation field or as the acceleration field because it is the term responsible for radiation and is proportional to the charge's acceleration. The other term, known as the generalized Coulomb field, dies out at large distances for all times. Thus, only an accelerating charge is responsible for electromagnetic radiation (or a changing current, which is composed of accelerating charges).

Visualizing Radiation

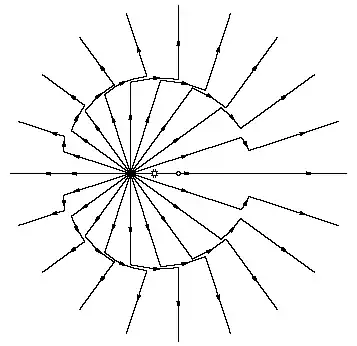
Here's a picture$^2$ of a charge, initially at rest, that accelerated quickly to some constant speed $v$. The circular curve sketched by the apparent discontinuity in the field lines is the front of the electromagnetic wave, which is traveling at a speed $c$. The electric field inside the circle is the "new" field produced by the charge moving at $v$. The outside field is the "old" field that was generated when the charge was at rest. Over time, the outside field is replaced by the new field.

---

References:

1. Introduction to Electrodynamics - David J. Griffiths
2. https://i.sstatic.net/PUvZx.gif

Answer 2

There are two possibilities to accelerate particles; often this are electrons, so I will talk only about them. First you can accelerate electron straight or in a curve in an electric or magnetic field. Second you can accelerate electron in a curve and with constant angular velocity. In both cases you interact with the electron with help of electromagnetic energy. When ever you interact with electrons you do this with help of photon exchange.

Doing this you level up the energy state of the electron. The electron try to get back to the ground level (the level of the surround particles). During positive acceleration some part of the photons (energy) remains in the electron and levels up his energy state. During negative acceleration more photons leave the electron.

Edit

How a radio wave leave his source you can see her https://en.wikipedia.org/wiki/Camille_Papin_Tissot

Answer 3

Yes, EM wave can be formed by electrons in constant velocity. As Maxwell said $$\vec{\nabla}\times \vec{B}=\mu_{0}J+\frac{1}{c^{2}}\frac{\partial \vec{E}}{\partial t}$$ Electron moving in constant velocity means a current. This current gives rise to a magnetic field. This is not instantaneous. This information travels with the speed of light. So at every point in space there is a change of magnetic field with time. This rate gives rise to Electric field as $$\vec{\nabla}\times \vec{E}=-\frac{\partial \vec{B}}{\partial t}$$ So we get a electric field and hence a elctro-magnetic wave. For more details please go though Feynman lectures. He explained it in more details.