Does or should the metric expansion of space imply a locally observable increase in kinetic energy?

Question

The title is the question. Here's why it seems like local kinetic energy should increase:

Numerous questions and answers here and elsewhere suggest that the reason the metric expansion of space is not observable locally (even on a galactic scale) is that local forces maintain the metric distance between near objects, with "near" meaning anything from two subatomic particles to two celestial bodies.

My mental picture is of ants on an expanding balloon. The ants get farther apart, but the expansion of the balloon beneath their feet is not going to tear the individual ants apart. They do however have to do a little dance to keep from doing the splits.

It seems to me that this should imply a continuously increasing kinetic energy, presumably generalized as random motion -- i.e. things get hotter.

Here is a simple illustration. A and B could be particles attracted by the electromagnetic force, or whole planets attracted by gravity:

1. A begin state with an arbitrary distance and energy level:

   

2. A little bit later, the two objects are farther apart, implying an increase in potential energy:

   

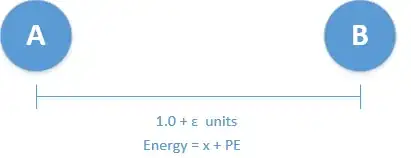
3. But the force at work brings the objects back to their original positions distance, implying the potential energy was converted to (kinetic?) energy through work W: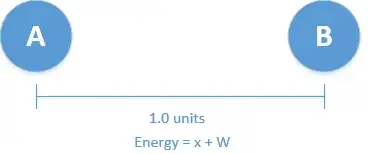

   

Obviously A and B don't actually wiggle apart and then back together, rather the force between them acts constantly as the metric expands constantly, implying a smooth increase in kinetic (or some other type) energy while the measurable distance between the objects stays the same.

Scenarios

1. Gravity at planetary distances: Jerry Schirmer's answer suggests the effect would be too small to measure
2. What about at subatomic scales? The color force between quarks in a nucleon is a distance-dependent force whose potential energy is orders of magnitude greater than gravity. Should metric expansion not cause an increase in energy of a individual nucleon, detectable as a few extra photons emitted over the course of some time?

Answer 1

The notion of kinetic energy is ill-defined in the spacetimes where you have a time-dependent cosmological expansion.

If you somehow attached two galaxies to each other with a spring, however, the expansion of the universe would do "work" against that spring, as there would be a force requied to keep the proper distance of the two galaxies fixed. At solar system distances, however, this would be completely undetectable.

Answer 2

The expansion does lead to a kinetic energy term that can be (at least partially) extracted. For objects that are bound to each other, it would lead to a classic acceleration term, which, of course, is equivalent to a classic pseudo-force. In an expanding universe, any two objects that are bound by a potential, are therefor experiencing an additional (albeit small) repelling potential term.

Answer 3

The expansion of the universe is not a force. Forces don't pull things apart at a particular speed; they change the speed by a particular acceleration. The speed itself is just inertia. It's no different in cosmology: there is nothing actively pulling things apart at the speed given by Hubble's law; that speed is just leftover momentum from the big bang, as modified over the intervening time by the attractive gravitational force and the repulsive cosmological constant.

To make this concrete, consider, say, two empty beer cans ($m = 15\,\mathrm g$ each) separated by $d = 1\,\mathrm{km}$ in outer space. Then we have

• Hubble's law separation speed = $H_0 d \sim 2\cdot10^{-15}\,\mathrm{m/s}$
• Gravitational attraction = $2Gm/d^2 \sim 2\cdot10^{-18}\,\mathrm{m/s^2}$
• Cosmological constant repulsion = $(\Lambda/3)d \sim 10^{-32} \,\mathrm{m/s^2}$ (I'm not sure about the factor of ⅓, but this is just an order-of-magnitude estimate. And I'm ignoring factors of $G$ and $c$ because there are no standard units for $\Lambda$.)

Although I quoted the Hubble's law velocity above, it is irrelevant. The only way the beer cans would have that relative velocity is if they coalesced directly from primordial hydrogen and helium, thus inheriting its average velocity, or if you deliberately gave them that relative velocity (which would be kind of like burying fake dinosaur skeletons). If they don't start out with that relative velocity, there is nothing that will make them tend to have it later. Sorry for all the boldface and italics, but this seems to be a very common misconception, possibly because of the misleading inflating-balloon analogy.

Of the two forces actually acting on the cans, the attractive one overwhelmingly dominates the repulsive one. So if these cans are initially at relative rest, they will very gradually start moving toward each other, not away.

These forces do perturb atomic energy levels and such, but the gravitational attraction again overwhelmingly dominates the cosmological repulsion, and even the attractive effect is undetectably small as far as I know. The Hubble recession does not affect atomic energy levels, not even a little bit.

You can extract energy from Hubble recession, but you're limited to the relative kinetic energy, as with any other relative motion. You can extract energy from gravitational attraction, but you're limited to the total potential energy. For cosmological repulsion, I think you can define a similar potential energy in de Sitter static coordinates, implying that the total energy you can extract from that over the lifetime of the universe is limited as well.