Are there two theories that are mathematically identical but ontologically different?

Question

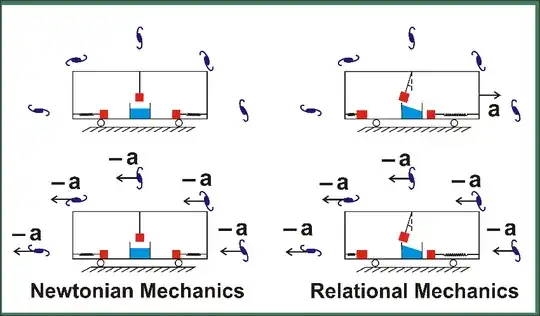
I have no background in physics but there is a question that has been bothering me, so I'm asking you.

Are there at least 2 physical theories that are :

• Mathematically identical, which means that they would yield identical predictions for EVERY situation that these theories can cover, and therefore can not be compared through experimentation : the validity of one of them is equivalent to the validity of the other.
• Physically different, that is to say, based on a different spatio-temporal-whatever realities, whose differences are not only semantic.

If there are at least two theories that satisfy those requirements, it would mean that the "absolute", "metaphysical" reality can never be known. However, if we are capable of mathematically demonstrating that such theories can not mathematically exist, it would mean that absolute reality can be known.

When I say "mathematically identical", I am not speaking of theories that can not be experimented on, due to technological constraints (like atomism at the time when this was still debated) but really of theories that can theoretically not be compared, even by a Laplace demon.

Do you agree with my assumptions? If so is there such theories and/or a demonstration that they can not exist?

Answer 1

Copenhagen quantum mechanics and DeBroglie-Bohm quantum mechanics, mathematically they are equivalent, "metaphysicaly" or "epistemologicaly" they are quite different

update The reason they are equivalent is because they reach the same central equation (Schrödinger equation) but from different paths. So the rest computations and experimental results can be calculated the same and so on.

Answer 2

Special relativity and Lorentz ether theory (LET). From the linked Wikipedia article:

Because the same mathematical formalism occurs in both, it is not possible to distinguish between LET and SR by experiment. However, in LET the existence of an undetectable aether is assumed and the validity of the relativity principle seems to be only coincidental, which is one reason why SR is commonly preferred over LET.

Answer 3

The other answers bring up some nice examples of theories in physics that are equivalent in prediction but different in interpretation. I just want to bring up a trivialized example to illustrate the flaw in the reasoning in the question.

Suppose I have two theories which each predict the same quantity, say the maximum temperature at a given location on Earth on a given day. To make this concrete, suppose the first uses sophisticated modelling of the atmosphere, weather processes, etc. Suppose the second one is a sophisticated statistical algorithm which makes its prediction based on a large sample of historical data, comparing temperature trends across decades and a wealth of other data.

And now suppose that both theories produce correct predictions. At first this seems implausible given the complexity of the system and the radically different approaches taken, but it's not so far-fetched that both produce correct predictions within the errors on those predictions.

How can you tell which theory is "correct" (probably more fair to ask which theory is "more correct than the other")? You could try to extend both theories to be more general and predict more quantities, and see which one starts to break down (or more likely, both break).

I think the more interesting underlying question is "Is there a unique theory that accurately predicts all physical processes?". First, though, one needs to settle the question of "Can a theory of everything exist?", see Gödel's incompleteness theorems (and also this) for some information on that topic.

Answer 4

Well, I can make a guess for the future. Suppose that we establish that a specific string theory incorporates the standard model, thus gives the same predictions and descriptions as the standard model, and includes quantization of gravity. This theory of everything (TOE) will be identical as far as observations and predictions go as the standard model and effective quantized gravity we now have as established. ( Big Bang Model).

The two theories have different metaphysical implications, standard model + effective quantized gravity aim to completely describe reality as we know it,no metaphysics, but string theory adds another six dimensions at least which could easily accommodate metaphysics in those dimensions.

Answer 5

Consider classical electrodynamics. Here you can introduce potentials $\phi$ and $\vec A$ from which you can derive the electric and magnetic field. However they are not uniquely defined by the electric and magnetic field, but different potentials can generate the same fields. Unlike electric and magnetic field, those potentials are usually not considered real, but just a mathematical tool to help describing electric and magnetic fields, because the observable behaviour is determined solely by the electric and magnetic fields.

But of course you can easily modify classical electrodynamics by just declaring those potentials as physical/ontological fields. Then the gauge freedom would mean that we cannot determine the actual values by observation, because as physical fields they would, of course, have to have unique, well defined values everywhere.

Now quantum mechanics gives this an interesting twist, through the Aharonov-Bohm effect: In this effect, a confined magnetic field affects the quantum phase of electrons where there's no electric or magnetic field, in a way visible through interference. Now if you assume that the potentials are actually physical fields, then the Aharonov-Bohm effect is completely local: You just integrate the vector potential along the way of the electron. However if you don't consider the potentials to be physical fields, then you'll find that Aharonov-Bohm is a non-local effect: The interference pattern of the electrons depends on the magnetic field in a region which the electrons never enter, not even in a quantum sense.

Note that also the Aharonov-Bohm effect is gauge invariant (indeed, we know that all of physics is); that is, you cannot distinguish different potentials leading to the same electric and magnetic fields by doing an Aharonov-Bohm experiment. Therefore also this experiment cannot distinguish between the two theories.

Also note that this "Aharonov-Bohm nonlocality" is independent from the nonlocality associated to Bell's inequality.

Answer 6

See http://en.wikipedia.org/wiki/Holographic_principle

N-dimensional classical gravity can be mapped onto N-1 dimensional quantum field theory.

Those worlds are very different. You'd think one or the other would have to be "true", but they're completely equivalent. If you think you live in one, the other is just a mathematical trick. But who's to say the other viewpoint isn't right and your perceptions are just being tricked?

Answer 7

Another example more close to our everyday experience is classical mechanics which recognise absolute motion through absolute space/time and relational mechanics which recognise only relative motion.

They are mathematicaly equivalent since in classical mechanics all measurable quantities are relative and/or differences between other quantities. Metaphysicaly or epistemologicaly they are quite different as the referenced link may convince you (check for example the PDF linked and consider the famous bucket thought experiment and the absolute-relational debate about space-time).