How can a metal heated at 600° emit thermal photons at 4000°+?

Question

Suppose we have a cube of metal inside a room at temperature 27°. If we heat the metal up to 600° using uniform radiation of that energy, no part of it should have higher T°, but nevertheless it will start emitting visible light, that is thermal photons with a temperature in the excess of 4000°. How is that possible?

I am aware of thermal radiation, blackbody etc., the first question is:

1) - when the metal is at thermal equilibrium with the room (27°) are there inside it or inside the room any molecules/atoms with energy in the range of 4000°? if the answer is affirmative the question has been fully answered, if is negative we need a follow-up question

Answer 1

If you heat a metal (or anything else) up to a temperature $T$ then the average energy of any degree of freedom of the metal will be of order $kT$. At 600ºC this is about 0.075eV, and as you say the energy of visible light is around 2 - 3eV, which is a factor of 30 or so higher.

The reason that visible light can be produced is because the thermal energy is randomly distributed. That means some bits of the metal will have substantially lower energy than 0.075eV and some bits will have substantially higher energy than 0.075eV. You get small parts of the metal where the energy is as high as 2 - 3eV, and it's those parts that are emitting the light.

The intensity of the emitted radiation is given by Planck's law:

$$ B(\lambda) = \frac{2hc^2}{\lambda^5} \frac{1}{\exp\left( \frac{hc}{\lambda k_B T} \right) - 1} $$

If you take your temperature of 600ºC (873K) and calculate the intensity as a function of wavelength using Planck's law you get:

so you can see the intensity peaks between 3 and 4 microns, which is in the infra-red. Looking at the graph the intensity appears to fall to zero at about 1 micron, which is still in the infra-red. However if you calculate the intensity at the wavelength of red light (0.7 microns) you find it isn't zero, but it's pretty small at about 0.002% of the peak intensity. So at 600ºC the metal will be producing a little red light.

Answer 2

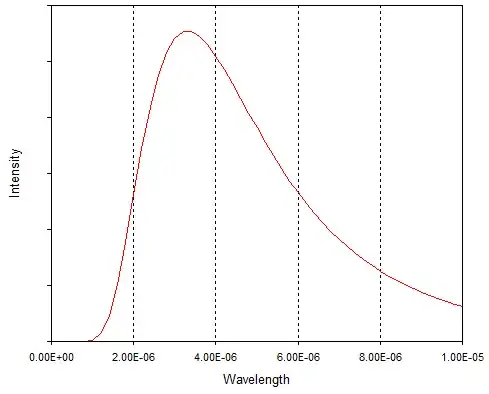
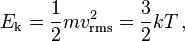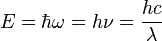This is the basic confusion:

but nevertheless it will start emitting visible light, that is thermal photons with a temperature in the excess of 400°.

Temperature is an intensive variable, it characterizes the whole sample.

Examples of intensive properties are the temperature, refractive index, density and the hardness of an object. No matter how small a diamond is cut, it maintains its intrinsic hardness.

Going into the statistical mechanics origins of this intensive property, one number measured by a thermometer, which emerges from the order 10^23 molecules of a sample, we see that temperature enters as the average kinetic energy of the molecules in the sample.

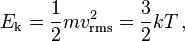
rms is the root mean square of the velocity. It means we take the whole sample of molecules and average its velocity to get the temperature as defined by thermodynamic quantities too.

The black body radiation curve has a wavelength range for its peak. One speaks of a 5000K distribution, for example which is the whole distribution of the energy of the photons emitted at 5000K. This peak moves to the right as the temperature falls, but all energies/wavelengths are available for the photons. The energy of the photons can range from zero to infinity.

So to identify the energy of a single photon with a black body temperature is a great stretch of imagination. What one is doing is saying: this single photon has the energy that the peak of the black body distribution has at 4000°. Since as John shows in the plot the distribution of the kinetic energies is continuous there will always be in the tails some photons of even very much higher energies.

How they can get these energies? The black body radiation is a many body manifestation, collectively there exist energy states of very high energy, though with low probability as the appropriate black body curve shows, which can be excited and then decay back emitting a high energy photon.

Edit after comment

1) - when the metal is at thermal equilibrium with the room (27°) are there inside it or inside the room any molecules/atoms with energy in the range of 4000°? if the answer is affirmative the question has been fully answered, if is negative we need a follow-up question

Again there is this misunderstanding "with energy in the range of 4000°"

Here are the black body radiation curves:

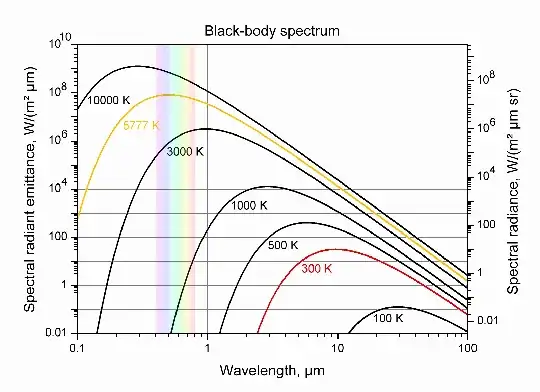
Please note that the relationship of temperature to kinetic energy is a statistical one, as I explained above, and the photon energy emitted by black body radiation ( reshuffling of the kinetic energies with loss into photons)

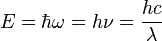
is given by a continuum of curves, one for each temperature, and each curve has a spectrum of photons from zero to infinity ( theoretically). It is a one (temperature) to many( photon energies) correlation. It is not one to one so as to be able to talk of a specific energy for 4000K. As you see all temperature curves cover the whole of wavelength i.e. energy. So the question has no meaning. The value of the energy of a specific photon can be as high as we want, a gamma ray for example, but it is the probability of emission that is very small ( shown as zero spectral radiance emittance in the plot on the left).

300K is the usual room temperature , and we see that the curve has infinitesimally small probability (note the logarithmic y axis) to emit a photon with wavelength smaller than a micron . Nevertheless, quantum mechanics being what it is, a probability exists, if one waits long enough, that an energy level of the collective lattice could be excited kinetically by the vibrations of the lattice and then decay with a high energy photon. At this level of probabilities though we are discussing the number of angels on the point of a needle.