0

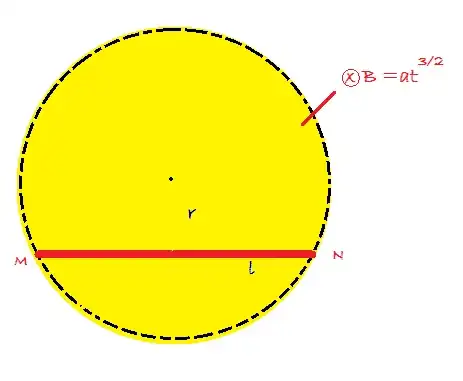
A metal rod of length $l$ is placed (as shown in figure) in a cylindrical time varying magnetic field. Find the potential difference across it. enter image description here

My answer:

As electric fields as forming circles around the centre with magnitude $$\frac12r\frac{dB}{dt}$$ whose magnitude is same along any chord at a fix distance from centre: $$\Delta V=E.l=\frac12r\frac32at^{\frac12}.l$$ $$\Delta V=\frac34arlt^{\frac12}$$

My question: Is $\Delta V =V_M-V_N$ or $\Delta V=V_N-V_M$ $\bf OR$ equivalently which side is at high potential?

Possible

  • $(i)$ As Field lines are circular from $M$ to $N$, $M$ must be high potential.

  • $(ii)$ As this field line apply a force on electrons- in the rod- towards left, then $M$ must have excess $e^-$ and $N$ must have deficiency; so $N$ would be high potential as $M$ is $(+)$ and $N$ is $(-)$.

Kyle Kanos
  • 29,127
RE60K
  • 725

1 Answers1

2

There is an electric field due to the changing magnetic field, which has direction left -> right.

Due to this field, there is an immediate charge seperation caused in the metal rod (-ve near M and +ve near N) which creates another electric field of equal magnitude and opposite direction to perfectly cancel the external electric field.

Thus the net electric field when going from M -> N is 0. Hence the potential difference is also 0. This is a very logical result considering the fact that the two points are connected by a perfect conductor (shorted).

You can always find the potential drop due to one of the electric fields. That should (must) give you potential drops of equal magnitude and opposite sign. But with this you can't say that one of the sides is at a higher potential. They are both at the same potential.

udiboy1209
  • 4,063
  • 1
  • 24
  • 39