What could cause an asymmetric orbit in a symmetric potential?

Question

My question can be summarized as:

Given a potential with a symmetry (e.g. $z\rightarrow-z$), should I expect orbits in that potential to exhibit the same symmetry? Below is the full motivation for this question.

A while back I came across an intriguing orbit (or rather class of orbits) that is not symmetric with respect to the $z=0$ plane in a potential with axial symmetry (axis along $z$) as well as symmetry with respect to reflection along the $z=0$ plane. Naively I would expect the symmetry of the potential to be reflected in the symmetry of the orbits, and this is the case in every textbook example I've seen, though admittedly I haven't done an exhaustive search through all classical mechanics texts.

The effective potential is:

$$\Phi_{\text{eff}} = \frac{1}{2}v_0^2\ln\left(R^2+\frac{z^2}{q^2}\right)+\frac{L^2}{2R^2}$$

It is drawn from Galactic Dynamics 2ed eq. 3.70 (see also fig. 3.3), and is a crude model of the potential of an oblate spheroidal galaxy with constant circular speed $v_0$. The parameter $q$ controls the axis ratio, basically how "squished" the spheroid is. For the examples I show below it's fixed to $q=0.7$.

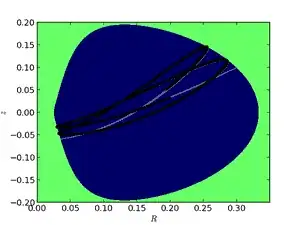
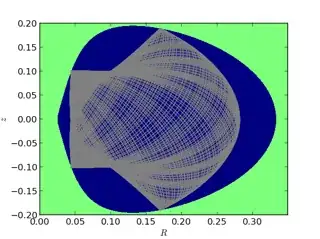
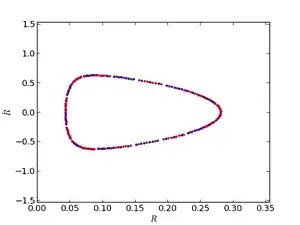
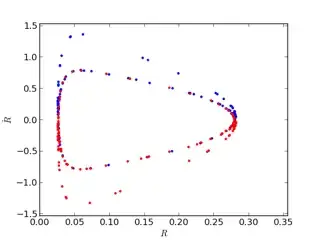
The azimuthal motion of the particle is essentially ignored - since a test particle in this potential just goes around the $z$ axis with constant angular momentum, this is easy to do. The effective potential still accounts for the angular momentum due to this motion, of course. By "following the particle" in the azimuthal direction, the motion can be described as a trajectory in the $R-z$ plane. In general, the motion of a bound particle (i.e. negative total energy) is expected to be confined to some region in this plane, the shape of which depends on the $L_z$ and $E$ of the orbit. Typical regions look like the top two panels here:

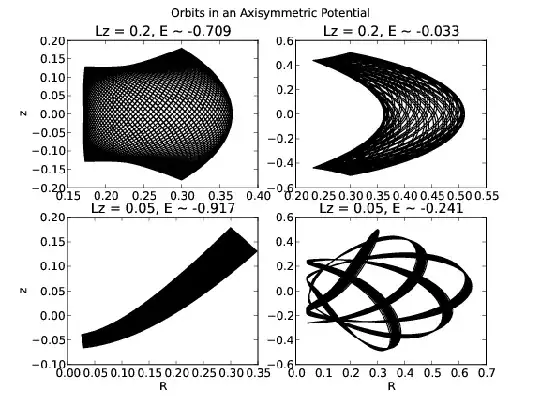
The lower right panel is also a typical orbit, but it fills in its "box" very slowly, so it looks a bit peculiar here.

The bottom left panel is the strange orbit I'm interested in. Notice that it fills in a well-defined region that is not symmetric about $z=0$. What's going on here? Why isn't the region symmetric about $z=0$ as my intuition suggests it should be? The orbital parameters $(E,L_z)$ are given above the plot. An equivalent way of expressing the orbital parameters is in terms of initial conditions. Example initial conditions that give an orbit qualitatively similar to the one in the plot:

$$R_0 = 0.3; z_0=0.1; \dot{R}_0 = 0; \dot{z}_0 = 0$$

Footnote regarding the numerics: Orbits were computed using the RK4 algorithm with a timestep of $0.002$. I've played around with the parameters (timestep, initial conditions, different integrators, etc.) to be reasonably confident that this is not a numerics issue. Furthermore, one of my colleagues has independently computed the same type of orbit, the only thing I provided was the expression for the potential and the ICs. Of course we may both be doing something wrong, but the probability for that is much lower than for just me having screwed up...

Answer 1

A simpler example is Kepler's laws of planetary motion. In a spherically-symmetric gravitational field, the planets follow elliptical orbits. The orbits certainly do not have the full spherical symmetry of the potential. They may be extremely lopsided. :-D

Answer 2

Symmetry of potential alone is not enough to guarantee a symmetric orbit. The initial and boundary conditions must also be symmetric. Also, for non-linear systems, numerical treatment has to be sufficiently accurate.

Answer 3

On the off chance there was any doubt about the numerics, I too wrote a code to follow these orbits. I use RK4 to take the first half timestep (a full timestep here is always $0.001$), and then perform the remaining integration via leapfrog.

Below is the evolution of an asymmetric orbit. The potential is given by $v_0 = 0.9$, $q = 0.7$, $L = 0.05$. I set the initial conditions to be $R_0 = 0.3$, $z_0 = 0.1$, $\dot{R}_0 = \dot{z}_0 = 0$, corresponding to a total energy of $E \approx -0.879$. The animation shows the orbit up to time $t = 360$. (The black points show the position over the last tenth of a frame.)

The orbit does not leave that select strip in the $(R,z)$-plane, even after very long integrations. What I find particularly thought-provoking in this plot is the background color. The blue region is that for which $\Phi_\mathrm{eff} < E$. Clearly the dynamics are restricted to a small subset of the kinematically accessible space, but of course we knew this had to be the case because the potential well is not asymmetric.

Consider now a symmetric orbit, shown below for $t < 100$. This is in the same potential and has the same $z$-initial conditions, but has $R_0 = 0.1$, $\dot{R}_0 = 0.90678050587096637$. This choice forces $E$ to be the same as in the last case.

Here the potential well shading is particularly telling. Even in this "well-behaved" case we are not exploring the full potential well kinematically accessible. Put another way, there are starting locations $(R_0,z_0)$ such that for any initial velocity $(\dot{R}_0,\dot{z}_0)$ consistent with the fixed $E$, no resulting orbit fills out quite the same region of the $(R,z)$-plane.

At first it seemed somewhat strange to me that two different initial conditions could fill two distinct but yet overlapping regions of the plane. But then I remembered this is really a 4D phase space $(R,z,\dot{R},\dot{z})$. Given an initial location in the phase space, the orbit will presumably fill some region, and no two distinct regions can intersect. It is only the projections of these regions onto $(R,z)$ that can intersect. From even the symmetric case it is clear there must be more than one such region, since the orbit didn't fill the whole potential well.

The picture I have in my mind then is of multiple disjoint regions of phase space, each corresponding to a family of initial conditions (equivalently the collection of all conditions encountered for a given orbit). There is symmetry in the layout of these regions, but not all project to symmetric regions in $(R,z)$. Rather, some come in pairs related via reflections about $z = 0$. This is not too surprising in and of itself I feel.

What is more intriguing than there being conjugate pairs of regions in phase space is that some regions are their own reflection-across-the-midplane conjugate. That is, as one varies the initial conditions from a singleton region (symmetric case) to one of a pair (asymmetric case), there must be a bifurcation of sorts.

To investigate this, I followed up on your surfaces of section idea mentioned in chat. Given initial conditions, I evolved the system up to $t = 100$. I then noted the values of $R$, $\dot{R}$, and $\dot{z}$ every time the $z = 0$ plane was crossed. Below is a movie showing the crossings in the $(R,\dot{R})$ plane, colored by the sign of $\dot{z}$ (blue for positive, red for negative).

At first crossings in both directions occupy the same 1D curve in the space. However, as the initial conditions are linearly changed from the symmetric ones given above to the asymmetric ones, some interesting things happen. A bifurcation occurs in the set of points, where two new branches appear, shown in the frame below. One new branch consists only of blue points, the other only of red. Very rapidly the original curve pinches off, leaving all upward crossings in their own 1D loop and all downward crossings in another.

This system transitioned rather rapidly (whatever that means). Other paths through initial condition space have given me plots that seem to vacillate between pre- and post-bifurcation before settling into the new pattern.

It is also worth mentioning that since the projection onto $(R,\dot{R})$ leads to a 1D section, and since the choice of $z = 0$, $R$, and $\dot{R}$ determine $\dot{z}$ up to a sign from simple energy considerations, the projection of the orbit onto the 3D $z = 0$ part of phase space is 1D.

I'm not sure how much I've answered the question so much as made some observations, but in summary:

• The kinematically accessible phase space is divided into dynamically inequivalent regions, not all of which project onto symmetric patches of position space even given the symmetry of the potential well.
• Asymmetric initial conditions can select such an asymmetric patch.
• There must be qualitative changes in the system's behavior at the bifurcations separating symmetrically-projecting and asymmetrically-projecting regions of phase space.