Electromagnetic waves are generally depicted like this:
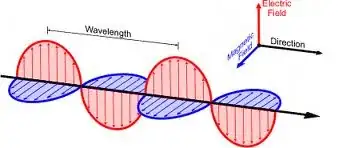
Where the electric fields and magnetic fields exist in the planes perpendicular to the direction of propagation. I also realize that as the electric field changes while the wave is propagating, a magnetic field is induced and vice versa (by faraday's and maxwell's laws of induction). But, those laws predict that the fields will be circular. So, won't the electric and magnetic fields look different? Won't they be circles along arrows that are drawn in the figure? I haven't seen anything written about this anywhere.