First I would like to give you a classical standard definition of a wave. But at the same try to keep in mind that there are different types of waves. Some are transverse waves such as electromagnetic waves and some are longitudinal or pressure waves such as sound waves. These different types might create the vagueness you describe. EM waves travel through a vacuum and sound waves and water waves do not as they require a medium. Now the Classical Wave definition to build from follows.
In the classic sense a wave is a disturbance that travels through a medium. It transports energy from its source to another destination while at the same time not transporting matter from the source to the destination. Each individual particle of the medium is temporarily displaced and then returns to its original location. And each particle transfers the energy disturbance to its adjacent particle in the same direction thereby propagating the wave.
The wave equations follow :
Mathematically, the most basic wave is the (spatially) one-dimensional sine wave (or harmonic wave or sinusoid) with an amplitude $u$ described by the equation:
$u(x,t)= $A$\sin$(kx-$\omega$t + $\phi$) ,
where
A is the maximum amplitude of the wave, maximum distance from the highest point of the disturbance in the medium (the crest) to the equilibrium point during one wave cycle. In the illustration to the right, this is the maximum vertical distance between the baseline and the wave.
$x$ is the space coordinate
$t$ is the time coordinate
$k$ is the wavenumber
$\omega$ is the angular frequency
$\phi$ is the phase constant.
The units of the amplitude depend on the type of wave. Transverse mechanical waves (e.g., a wave on a string) have an amplitude expressed as a distance (e.g., meters), longitudinal mechanical waves (e.g., sound waves) use units of pressure (e.g., pascals), and electromagnetic waves (a form of transverse vacuum wave) express the amplitude in terms of its electric field (e.g., volts/meter).

Sinusoidal waves correspond to simple harmonic motion.
The wavelength $\lambda$ is the distance between two sequential crests or troughs (or other equivalent points), generally is measured in meters. A wavenumber $k$, the spatial frequency of the wave in radians per unit distance (typically per meter), can be associated with the wavelength by the relation
$k=\frac{2 \pi}{\lambda}$ ,
The period T is the time for one complete cycle of an oscillation of a wave. The frequency f is the number of periods per unit time (per second) and is typically measured in hertz. These are related by:
$f=\frac{1}{T}$ ,
In other words, the frequency and period of a wave are reciprocals.
The angular frequency $\omega$ represents the frequency in radians per second. It is related to the frequency or period by
$\omega = 2 \pi f = \frac{2 \pi}{T}$ ,
The wavelength $\lambda$ of a sinusoidal waveform traveling at constant speed $v$ is given by:
$\lambda = \frac{v}{f}$,
As mention this equation satisfies a wave in one dimensional space.
For Examples :

About 10 years later a more complete wave equation emerged considering multidimensional space.
The wave equation is a hyperbolic partial differential equation. It typically concerns a time variable $t$, one or more spatial variables $x1, x2, …, xn$, and a scalar function $u = u (x1, x2, …, xn; t)$, whose values could model, for example, the mechanical displacement of a wave. The wave equation for u is
${ \partial^2 u \over \partial t^2 } = c^2 \nabla^2 u$
where $∇2$ is the (spatial) Laplacian and $c$ is a fixed constant.
Solutions of this equation describe propagation of disturbances out from the region at a fixed speed in one or in all spatial directions, as do physical waves from plane or localized sources; the constant c is identified with the propagation speed of the wave. This equation is linear. Therefore, the sum of any two solutions is again a solution: in physics this property is called the superposition principle.
Multispatial Example :
EM Waves :
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum. It is a three-dimensional form of the wave equation. The homogeneous form of the equation, written in terms of either the electric field $E$ or the magnetic field $B$, takes the form:
$(c^2\nabla^2 - \frac{\partial^2}{\partial t^2})$ $\mathbf{E}$ = $\mathbf{0}$
$(c^2\nabla^2 - \frac{\partial^2}{\partial t^2})$ $\mathbf{B}$ = $\mathbf{0}$
where
$c = \frac{1}{\sqrt {\mu_0\varepsilon_0}}$
is the speed of light in a medium with permeability (μ0), and permittivity (ε0), and ∇2 is the Laplace operator. In a vacuum, c = 299,792,458 meters per second, which is the speed of light in free space.1 The electromagnetic wave equation derives from Maxwell's equations.
Now that I have given you a little background on waves and pointed out especially that their are different types of waves, EM, Sound, those that require a medium those and those that don't. And noting that some propagate from a point source in one direction while a pressure wave could propagate in all directions. And the noting that the cause of waves can be due to different types of disturbances it should be a little easier to imagine one equation will not work for all types, propagation sources, and different dimensional propagations. It should also be noted that anumber of other factors would impact the math as well, boundary conditions comes to mind.
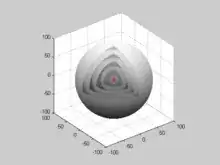
Also another important class of problems occurs in enclosed spaces specified by boundary conditions, for which the solutions represent standing waves, or harmonics, analogous to the harmonics of musical instruments.
The wave equation, and modifications of it, are also found in elasticity, quantum mechanics, plasma physics and general relativity.
So to get a handle on which mathematical model you need to work with you need to first
pick what wave you want to discuss and what and how the disturbance was sourced and into how many spatial dimensions, does the medium need to be considered or is it traveling in a vacuum and will a classical treatment suffice or does general relativity suffice or perhaps we need to use quantum mechanics to drive the solution home.
An Example of a Boundary Condition like a drum.
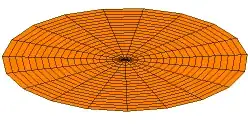





 GNUFDL image by Kraaiennest, see
GNUFDL image by Kraaiennest, see 