Bending of light from a moving light source

Question

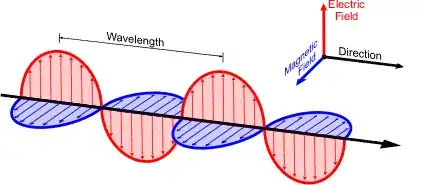
First I will have to explain my question. Look at the image below. This shows doppler shift when an object is moving horizontally to the direction of the wave. Keep the word 'horizontally' in mind. Now this happens because:

I will quote Jim from his answer for Redshifting of light from a moving light source

We all know that light is a wave, when you turn on your headlights and drive in reverse, the light is doppler shifted because of the motion of source. When not moving, each cycle of the light wave is emitted from the same position; it has a specific set of wavelengths. The distance between one crest of a wave and the next crest is equal to the speed of light, c, times the period of the light (which is determined by the oscillations in your headlights and won't change when you are in motion). When you drive backwards, the distance between one crest and the next becomes the period times c plus the period times your backwards velocity (approximately); the second crest is not emitted at the same location as the first, so it extends the wavelength. From your perspective, the emitted wave would not be red-shifted at all, but from a stationary observer's perspective it is.

So now my question is, imagine a car which has a torch attached to one of its windows. The torch is switched on and the car begins to move. When the car moves, its movement is in the opposite axis from the propagation of the wave. So each crest will be released from a different location while the first crest is already on its way in a straight line. I will try to represent this graphically.

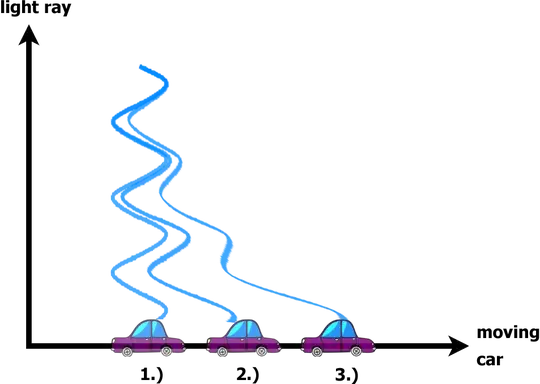
The representation is very estimate. It just shows how would the light bend as each crest is released from a different location. Please explain this to me. Will the light actually bend? Why or Why not?

Edit

What I have concluded from the answers is that first a photon is emitted and then it continues as a wave and is in no way attached to other photons. Is this right? If I got this then I got the answer for my question.

Answer 1

The light is not bending, although the paths you draw appear as if they do. If you treat the light as a photon (because of wave-particle duality), you will see that the newly emitted photons are simply emitted at an offset from each previous one. Thus the wave isn't bending, it's simply being generated by a source at a different location. Evaluated in extreme conditions (i.e. when v_car -> c), relativistic effects may begin to be relevant, but those seem to be beyond the scope of the question.

Answer 2

The light will not bend. The blue line is not the trajectory of the light ray (whether you view it as a wave or a photon does not matter), it represents the distribution of electric and magnetic fields at a certain point in time. View it as a snapshot of the wave, if you like. What you have drawn is a simplified version of this diagram:

The arrow labelled "Direction" does not represent the wave's path as a function of time, but the wave's spatial extent at a certain point in time. Even if this spatial distribution is "bent", that does not mean that light follows a curved trajectory.

Answer 3

The excentrical Doppler effect is not an easy problem. It has afaik no analytical solution (if you employ special relativity). In the classical limit it might be easier.

Since you want the light to be treated as wave, you also need to throw away notion of "bending". A wave spreads out in every direction from every point. A light ray is just superposition of point waves into a wave front. "Bending" of light makes more sense when you talk about photons.

Perhaps this will become clearer if you follow try to calculate the classical!Doppler effect:

Let's look at the crests the torch produces. If the car moves at constant velocity, the origin of crests will be equally spaces on the car's path (your x-axis). Let's say a crest is produced on every meter, with the car going one meter per second. Then the time a crest needs to arrive at the observer is $\Delta t_x=\frac{1}{c}\sqrt{e^2+x^2}$, where $c$ is the speed of light, $e$ is the excentricity of the observer (how far he is from the car's path) and $x$ is the distance the car has travelled.

Since the crests are not sent all at the same time, we have to add that time to the time of sending: $t^{\text{sent}}_x=\frac{x}{v}$ where $v$ is $1\frac{m}{s}$. The time of arrival thus is $t^\text{arrival}_x = \frac{x}{v}+\frac{1}{c}\sqrt{e^2+x^2}$. The frequency of sending light is 1Hz (one crest per second). The frequency the observer will perceive is the inverse of the difference between two crests: $$ f_x = \frac{1}{t^{\text{arrival}}_{x+1}-t^{\text{arrival}}_x} $$ Which is a rather complicated expression. :( But fortunately the computer can visualize it:

Answer 4

Your drawing has some mistakes: the wave is not spatial in that sense, the peaks and valleys are a representation of the strength of the electric (and or magnetic) field at that position. So, your light ray should be unidimensional. For instance, the actual wave for the car at rest should be a line, the light will not move back and forth as it travels up. Plus in addition, in you drawing you are implicitly assuming a classical addition of velocities by assuming that the wave behaves non-relativistically. It is an axiom of special relativity that any observer will perceive the light as moving stight and at the same speeed regardeless of the motion of the source of the light. All weird effect of relativity start at this assumption. So, both observers will see a ONE-dimensional light ray moving along a straight path: the locations of the peaks within that line will have nothing to do with the perceived path.

Answer 5

rahulgarg12342,

Looks like either your description or your drawing is misleading. You say that the torch is fixed to the car and sends light beam perpendicular to the direction of the movement, and yet on the drawing the torch seems to be hand-held and directed at particular point on the ground, and so the angle keeps changing all the time.

Anyway, whatever you had in mind, your puzzle can be solved by using the Principle of Relativity and assuming it is the ground moving, and not the car. In such case the light beam is always a straight line. And if the torch is just fixed, as you said, the light is sweeping the surroundings all the time.

(In case the torch was actually meant to be hand-held and changing the angle. Remember one thing: when we are watching a light beam in the dark we are just seeing a multiple of photons - each being also a wave itself - and not a single wave that goes all the way from the torch to the destination point. Also when it looks as if we are seeing the photons as they are traveling, all we can actually see are the photons that never made it to the destination point. What we can see are only photons reflected back toward our eye by particles (of air), and therefore those photons never reached "the end", unless they got reflected off the end-point, but still, we cannot see their route. We cannot see see a photon "on its way" from afar, because in order to see a photon it must come directly to our eye.)

If you clarify your question a little bit, I will be able to elaborate more.

Answer 6

Other answrs havent covered effect of Coriolis force on the emitted waves. Light bends here because of Coriolis force on the waves because of the rotation of the earth, just like you twist and fall from your bicycle when it is moving. In book situations our teachers always give us simplified situatons, but life is considerably complex.