I will use this reference Chapter 3 Time dilation from the classical wave equation from Understanding Relativistic Quantum Field Theory by Hans de Vries
3.1 Signal propagation: The bouncing photon clock
The classical wave equation tells us that the propagation is on the light
cone, and the propagation speed is c. With this as a starting point we will
show that we should expect that physical processes which move progress
slower as they do when at rest.
With the help of a Bouncing photon clock and beautiful pictures (Figure 3.1: Bouncing photon clock, at rest (left), moving (right))
he analyses two configurations (bounce vertical or horizontal irt the motion) to show that...
His explanation is so simple, and the graphics are so clear, that one deserves to consult that document.
EDIT ADD :
to ease the interpretation I'will post that figure along with some words:
situation A
on top left: a clock A at rest, distance between faces is always L, even when in motion
on top right: the same clock A in motion with v velocity to the right
”tick” and the ”tock” are equal in duration, being 'tick' the time interval for the photon to move from the top to the bottom mirrors and 'tock' idem from bottom to top;
The photon moves on the diagonals (the arrows) with the speed of light
c The vertical component of the speed which determines the duration of
the ticks is thus $\sqrt{c^2-v^2}$ and the duration of the ticks for a
distance 2L between the mirrors becomes:
$T_{tick}+T_{tock}=\frac{2L}{\sqrt{c^2-v^2}}=2\gamma L/c$
situation B - The two bottom images
In the case, where the photon bounces horizontal we get an asymmetry.
The photon moving along with the mirrors in the same direction takes
more time to go from one mirror to the other as the photon moving in
the opposite direction as the mirrors. The times$T_{tick}$ and
$T_{tock}$ are different.
$T_{tick}+T_{tock}=\frac{\lambda/L}{c-v}+\frac{\lambda/L}{c+v}=2\gamma L/c$
However, in both cases the total time for the tick plus the tock is $=2\gamma L/c$,compared with a total time of $=2L/c$ for a clock at rest. In both cases the clock runs slower by a factor $\gamma$. The factor $\gamma$ which determines the time dilation.
Notice the agreement with the text of Einstein(1905)
Note: a longer time interval, as compared to the one at rest, to perform the same TickTack, correspond a slower clock rate.
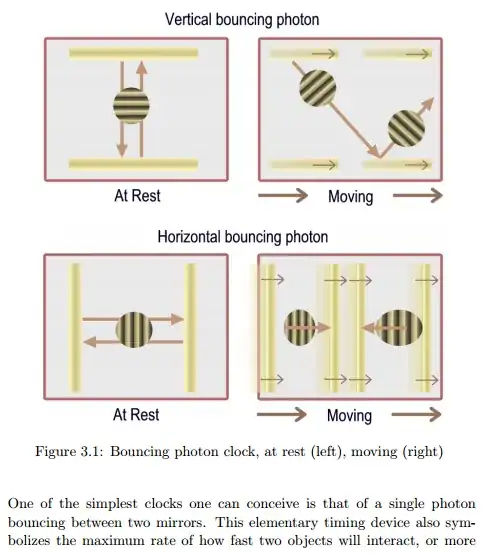
To avoid incorrect interpretations I will decompose the bottom right image in two, corresponding to the same mirror B at time $t_0$ (photon moving to the right) and time $t_0+\delta t$ (photon moving to the left, after reflection)
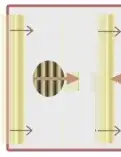 and
and 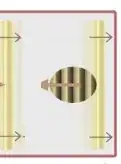
The document deserves a closer attention, finally, it explains the Twin paradox
Closer observation of figure 3.1 shows that the wave length of light changes
when .... the Doppler effect on the photons ...
... Even more interesting are the diagonal wavefronts
(this video 'Theory of relativity explained in 7 mins' at 1'30" can clear your mind, I hope)


