I am struggling with calculating the exclusive semileptonic $B_c^+\rightarrow J/\psi l^+\nu_l$ decay. I learnt that the amplitude is given by a product of the leptonic current $L^{\mu}$ and the hadronic current $H^{\mu}$ $$ \mathcal{M}(B_c\rightarrow J/\psi l^+\nu_l)=\frac{G_F}{\sqrt{2}}V_{cb}L^{\mu}H_{\mu} $$ where $V_{cb}$ is the CKM parameter, $L^{\mu}$ and $H^{\mu}$ are expressed as $$ L^{\mu}=\bar{u}_l\gamma^{\mu}(1-\gamma^5)v_{\nu},\quad H^{\mu}=\langle J/\psi|J^{\mu}(0)|B_c\rangle $$ where $J^{\mu}$ is the $V$-$A$ weak current. However, I did not know how this result can be derived. Could anyone provide some help?
There is a second problem. On the tree-level, we have the following Feynman diagram
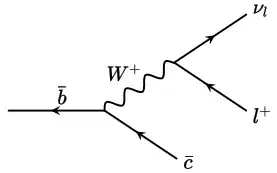
If we calculate $\bar{b}\rightarrow\bar{c}l^+\nu_l$ as a three-body decay in the electroweak theory (not the four-fermion approximation adopted above), how does it relate to $B_c^+\rightarrow J/\psi l^+\nu_l$?