Why is absolute zero considered to be asymptotical? Wouldn't regions such as massive gaps between galaxy clusters have temperatures of absolute zero?
I just do not see why our model must work the way that it does. I mean there have to be regions with no thermal energy out there, the universe is massive.
We can only approach absolute zero asymptotically because we can't suck heat out of a system. The only way we can get heat out is to place our system in contact with something cooler and let the heat flow from hot to cold as it usually does. Since there is nothing colder than absolute zero, we can never get all the heat to flow out of a system.
We can reduce the temperature by increasing the size of the system and diluting the heat. In fact this is why the CMB (cosmic microwave background) temperature is only 2.7K rather than gazillions of K as it was shorlty after the Big Bang. The expansion of the universe has diluted the heat left over from the Big Bang and reduced the temperature. However achieving absolute zero this way would require infinite dilution and therefore infinite time, which is why the universe approaches absolute zero asymptotically.
Actually, assuming the dark energy doesn't go away the universe will never cool to absolute zero even given infinite time. This is because the accelerated expansion caused by dark energy creates a cosmological horizon, and this produce Hawking radiation. The Hawking radiation will keep the temperature above absolute zero.
Classical physics (intuitive) answer: temperature is a property of matter, that is a sort of estimate of the kinetic energy of particles. If you have no particles, there's nothing to measure the temperature of.
Mathematical answer: since temperature is changed by multiplying by a real number, the only way to reach 0 would be to have an object already at zero to begin with which would suck all the surrounding energy. This object has not been found to my knowledge (apart from gravitational singularities, and there are doubts about their existence).
Current physics has established that the underlying framework is quantum. A basic principle of quantum mechanics is the Heisenberg Uncertainty Principle, HUP.
This ensures that for particles there can be no exact measurement or condition of 0 kinetic energy, so an ensemble of particles cannot have definite temperature of 0.
Photons are also particles and permeate the observable universe, even the emptiest of space, this is known as the left over radiation from the time that the universe became transparent to the electromagnetic waves . It is called cosmic microwave background, CMB, and its average energy is 2.7K.
This is what we observe:
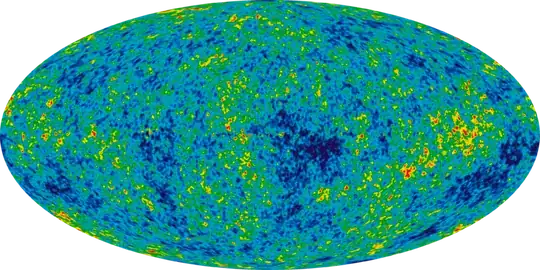
All-sky map of the CMB, created from 9 years of WMAP data
There is no zero, although there exists a cold spot:
The "cold spot" is approximately 70 µK colder than the average CMB temperature (approximately 2.7 K), whereas the root mean square of typical temperature variations is only 18 µK.
Thus, even if our universe is huge , there does not exist a spot without photons , and the HUP will ensure that there exists no zero K temperature.
Please also to remember that quantization of gravity will fill the space with gravitons, which will also be elementary particles and carry some energy, no matter how small, and will obey the HUP too. So in any interesting Universe there can be no 0K .
In thermodynamics, temperature is defined from the zeroth law (yes, they thought of this after the first, second and third... - then realized they had forgotten something pretty fundamental). The zeroth law is this:
If system A is in thermal equilibrium with system B, and system B is in thermal equilibrium with system C, then system A is in thermal equilibrium with system C.
This is a fancy way of saying "temperature exists". But it also says "temperature exists when something can be in equilibrium with something else".
Thermodynamics really only deals with large scale response of a system - when you go down to the individual particle level you look at the kinetics of particles, and make statements about the "temperature" based on the average kinetic energy.
No region of space is "forever empty". While there might exist at any one moment in time a large region of space without particles in it, you can't actually know that it is empty - and the moment you discover it is not empty, you will have encountered a particle. If that particle was truly stationary (in which case - how did you come across it?), the act of measuring it will have imparted some momentum (uncertainty principle) so it's not at rest any more.
In other words - macroscopically you can't tell that an empty region of space has "zero" temperature; and microscopically, any attempt to measure zero will make it "not so".
The Universe is pervaded by the cosmic microwave background radiation, which has a temperature of $2.7$ K. Any region in the Universe must have at least this temperature.
An empty space wouldn't have any particles to "be hot", but there would still be EM radiation of various wavelengths. Since no place can be infinitely far from any source of EMR, the radiation level can never drop all the way to 0. The CMB is everywhere, anyway.
Now, if there is no matter around, what are you taking the temperature of? You could just as easily claim that the temperature is infinite as it is 0 K. You need to carefully define just what it is that you're looking at the "temperature" of.
Quantum mechanics and the uncertainty principle (which just answered a while ago) states that consituting particles of a system have to undergo movement (change of state), else they could be localized with arbitrary precision.
Absolute zero temperature by (classical) definition is the temperature where a system is a "perfect crystal" (the energy state of a certain symmetry and nothing moving or changing further).
So combing the above 2, the result follows that absolute zero is asymptotical.
Quantum mechanically, even the ground state of the "void" is not at zero temperature, but can indeed exhibit fluctuations.
UPDATE:
Check this question regarding a further connection between quantum uncertainty principle and thermodynamics.
There has been many answers to that question and my answer will be probably lost in the sea of responses and different opinions. However, as it departs significantly from the proposed view points I might sketch it here.
Recent debates about heat flows, negative temperatures and the notion of entropy in statistical thermodynamics have allowed to raise questions about the notion of temperature. In particular, the negative temperatures (which although still debatable are quite well defined) seem to contradict the fact that zero temperature cannot be achieved. It also contradicts the intuition since negative temperatures are hotter than infinite temperatures which kind of does not make sense when said like that.
It turns out that none of these conceptual inconsistencies occur if instead of looking at temperatures, we look at inverse temperatures often denoted $\beta = 1/(k_B T)$.
In this case, heat always flows from low $\beta$ values to higher $\beta$ values regardless of their sign. Also the concept of absolute zero corresponds to an infinite value of $\beta$ and since there is no end to infinities, there is also no end to approaching absolute zero without never reaching it.
I think this is the most sound and simple explanation to your question.
