Velocity distribution in ion source (electron bombardment) for Bainbridge mass spectrometer

Question

Consider the following schematics of a Bainbridge mass spectrometer

_{(Source: http://www.schoolphysics.co.uk/age16-19/Atomic%20physics/Atomic%20structure%20and%20ions/text/Mass_spectrometer/images/1.png)}

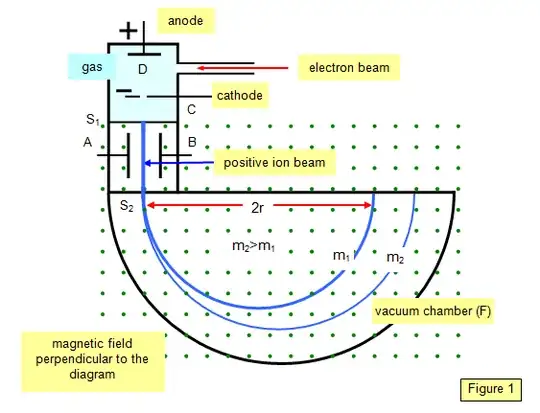
Suppose the gas contains two sorts of atoms (for example two isotopes of one element) with different masses. The electric force between the electrodes of in the gas chamber which accelerates them is $qE$, where $E$ is the electric field and $q$ the charge of the ions. For simplicity consider the case that you have one ion of sort A and one of type B each with equal charge q, but different masses $m_A$ and $m_B$ with $m_A > m_B$. Then the velocity of the $A$ before entering the Wien-filter will be smaller than hat of atom $B$ (because of it's mass). Furthermore suppose that the Wien filter only lets pass particles with velocity $v_A$, which is by assumtion the same as the velocity of our atom $A$. Because $B$ is faster than $A$, ions of type $A$ will pass the Wien-filter, but ions of type $B$ will not.

But then the magnetic field after the Wien-filter would be useless, because only ions of type $A$ would pass the filter.

So I guess that there must be another reason why the velocity distributions of type $A$ and $B$ atoms overlap after leaving the ion source such that both types $A$ and $B$ could reach the magnetic field after the Wien-filter.

Why is this the case? How can one quantitatively estimate how large the difference of $m_A$ and $m_B$ may be such that the velocity distributions of $A$ and $B$ overlap? Can you give me a quantitaive example of $A$ and $B$ and the concrete velocity distributions from experiments?

I am also looking for good references where those questions are discussed.

Answer 1

The Wien filter isn't infinitely precise. It will allow a small distribution of velocities thorough.

To review, the Wien filter works by setting up mutually perpendicular electric and magnetic fields. The value of these fields are set so that particles with the speed you want have no net force, and pass directly through the filter. Any particle with a different speed will experience a net force, and will be deflected away from the straight trajectory. A physical barrier and the exit of the filter prevents those deflected particles from continuing to the main part of the spectrometer. The particles that aren't deflected pass through a slit in the barrier.

The Lorentz force on a given particle in the Wien filter is $\vec{F} = q(\vec{v}\times\vec{B} + \vec{E})$. Assuming the velocities and the magnetic and electric field are all mutually perpendicular, and using your notation, this gives $v_A B = -E$ for a particle that passes straight through the filter with no deflection. So if we assume all particles are travelling in the same direction, we can let a general speed be $v = v_A + dv$. The force on a particle with such a speed is then $\vec{F} = q(\vec{v_A}\times\vec{B} + \vec{E}) + q\vec{dv}\times\vec{B} = qB(dv)$.

Say that the filter has a length $l$ in the direction of the particles' travel, and that the slit has a width $d$. Then applying the kinematics to a particle of mass $m$, we get that any particle with a speed such that $$\boxed{dv \leq \left(\frac{2v^2m}{l^2qB}\right)d}$$ will be allowed through the filter into main region of the spectrometer. You might be able to derive a relation between $v$ and $m$ based on the physics of the ion creation, but this works in general.

So why would you even want to do this two-step sifting process, anyway? The point of the initial filter is to narrow the range of particles that you're looking at. You then use the main part of the spectrometer to look more precisely at that set of particles. One typical use of mass spectrometry is to measure the abundance of different isotopes of a given element. In that case, the isotopes are your particles $A$ and $B$, and you want both of them to pass through the filter. You filter everything else, then optimize the main part of the spectrometer to distinguish between those two particles.