Tsiolkovsky figured it all out more than 100 years ago :)
Tsiolkovsky describes a cylindrical space ship: 100 meters long, 4
meters in diameter, rotating end-over-end about its "central
transverse diameter", with an endpoint velocity between 1 and 10
meters per second, producing an angular velocity between
(approximately) 0.2 and 2.0 rotations per minute, and a gravity level
between 0.002 and 0.2 g. These numbers were chosen to illustrate a
concept, and should not be taken too seriously. Nevertheless, they
show that Tsiolkovsky understood the problems associated with high
angular velocities, and the practicality of artificial gravity levels
of less than one full g.
When you stand on the ground of the station, you are moving at the speed of the endpoint velocity, let's say 10 m/s. When you jump at the speed of 1 m/s, your velocity becomes $\sqrt{1+100}$, but its direction is slightly inwards now. So, you're going to hit the floor again, but slightly off the point from where you jumped. So, you really are not pulled by the ground, but rather get hit by the ground.
UPDATE: here's the code and a plot to demonstrate what happens when a man jumps vertically at speed of 1 m/s, inside the spaceship of 100 m radius and endpoint velocity 10 m/s. The result is that a man will land 13 cm off the point he was initially in about 2 secs.
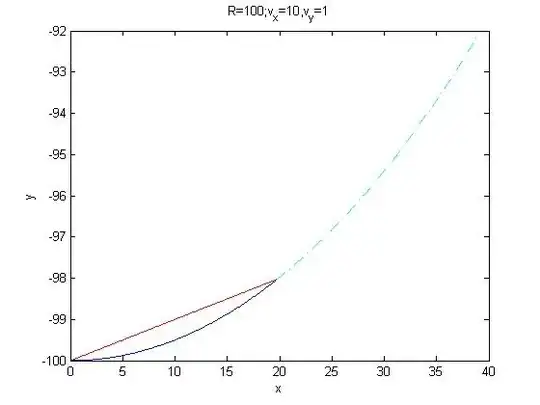
R=100;
ax0=0
ay0=-R;
vy=1;
vx=10;
phi=vx/(R) % angular speed
theta = (pi-2*( pi/2-atan(vy/vx)) ) % angle at hitting floor
bxf = R*sin(theta);
tau = bxf / vx % time to hit floor
axf = tau*phi; % angle the weel turns
d=(theta-axf)*R %distance from hit
t=(0:0.01:tau);
bx=ax0+vx*t;
by=ay0+vy*t;
plot(bx,by,'r')
hold on
ax=R*sin(phi*t);
ay=-R*cos(phi*t);
plot(ax,ay)
tau2 = theta/phi
t=(tau:0.01:2*tau2);
ax=R*sin(phi*t);
ay=-R*cos(phi*t);
plot(ax,ay,'-.c')
xlabel 'x'
ylabel 'y'
title 'R=100;v_x=10,v_y=1'
